Как посчитать площадь треугольника

Как высчитать площадь комнаты, в которой есть в наличии ниши и выступы?

Что делать, если в помещении имеются различные ниши или колонны, которые не могут быть скрыты или демонтированы? В этом случае с подсчетами придется немного повозиться, так как из значений общей площади придется вычислять те показатели площадей, которые занимают эти самые колонны, и добавлять к результату площадь каждой ниши.

Расчет площади комнаты с вырезом

Удобнее всего в этом случае на бумаге изобразить точную форму комнаты с указанием всех выступов, ниш и колонн. Далее производятся замеры длинных и ровных сторон помещения и записываются в соответствующем месте на листочек. После этого измеряется периметр каждой колонны и по выше указанной формуле (S = A х B) высчитывается площадь каждой колонны. Далее отдельными блоками по такому же принципу вычисляются параметры площади каждой ниши.

Далее все просто – считается основная площадь, т. е. длина и ширина самых длинных стен перемножаются. От полученного значения вычитаются площади колонн, а затем к результату прибавляются показатели площадей ниш. Получаем точную площадь всей комнаты.

В отдельных случаях (например, комната выполнена в форме буквы «Г») можно визуально разбить помещение на несколько ровных фигур (например, прямоугольников), снять мерки каждой фигуры отдельно, затем вычислить площадь каждого элемента и суммировать все полученные значения.

Г-образная квартира-студия

Как разграничить общую и жилую площадь квартиры

Многие люди рано или поздно сталкиваются с новостью, что, оказывается, площадь квартиры – это не однородное понятие, а весьма сложное и составное. Это для них оказывается сюрпризом, и нередко неприятным.

А между тем знать, какие бывают площади, чем друг от друга отличаются и как этим нужно пользоваться – весьма полезная и даже необходимая информация.

Например, чем отличается балкон от лоджии? Ванная и кухня к какой категории относятся? Все эти вещи следует знать.

Самым распространенным случаем, когда знание того, как считается площадь квартиры, очень помогает, а незнание становится роковым – это покупка квартиры с долевым участием. Нередко застройщик пытается зачесть лоджию в общую площадь квартиры, увеличив, таким образом, ее стоимость. Чтобы быть готовым к такому повороту событий первым делом нужно уяснить, что квартира имеет три разные площади:

• жилая площадь квартиры;
• площадь квартиры;
• общая площадь квартиры.

Правила и нормативы определения общей площади помещений регулируются Жилищным Кодексом РФ, в частности ст.15, п. 5, а также Инструкцией о проведении учета жилищного фонда в Российской Федерации (утв. приказом Минземстроя РФ от 04.08.1998 г. № 37).

Жилая площадь – это сумма площадей жилых комнат. Общая площадь квартиры – это сумма площадей всех комнат, составляющих данную квартиру, в том числе подсобных помещений, кроме лоджий, балконов, веранд и террас.

К подсобным помещениям относятся площади кухонь, коридоров, ванных, санузлов, встроенных шкафов, кладовых, а также площадь, занятая внутриквартирной лестницей.

Теперь понимаете, чем балкон отличается от лоджии? Лоджия имеет боковые стены, потолок и как бы утоплена в здание, а балкон выступает за периметр дома. И расчет их площади происходит по-разному. Эти на первый взгляд лишние и непонятные различия имеют далеко идущие юридические последствия, так что не пренебрегайте ими.

Обманувшиеся дольщики

Исходя из этого, нужно быть очень внимательным при покупке квартир по договору долевого участия.

Дело в том, что проектирование и строительство многоквартирных жилых зданий осуществляются на основании норм СНиП 31-01-2003, в котором расчет площадей предлагается производить согласно Инструкции о проведении учета жилищного фонда.

Но важно знать, что расчет стоимости квартиры регламентируется уже договором долевого участия, а в нем может быть записана какая угодно категория площади. Это может быть жилая площадь, тогда цена квартиры будет выше

Но компания может брать за основу общую площадь, тогда квадратный метр будет стоить меньше, в этом случае застройщик возьмет свое за счет большей квадратуры

Но компания может брать за основу общую площадь, тогда квадратный метр будет стоить меньше, в этом случае застройщик возьмет свое за счет большей квадратуры.

https://youtube.com/watch?v=NgDqPHEJe7Y

Чтобы не попасть впросак, то есть, чтобы не думать, что вы платите только за жилую площадь, а в итоге вам выставили счет за общую, следует внимательно изучить договор долевого участия.

В частности, обратить внимание, какая площадь квартиры идет в зачет. После всего доказать свою правоту будет крайне сложно

Только если реальная площадь квартиры будет отличаться от указанной в документе, можно заставить застройщика вернуть деньги

Только если реальная площадь квартиры будет отличаться от указанной в документе, можно заставить застройщика вернуть деньги.

На что влияет метраж квартиры

№ 307) для начисления платы за отопление учитывается общая площадь жилого помещения за исключением неотапливаемых помещений. Так что балкон, лоджия, кладовые, в отличие от туалета, коридора, кухни, не входят в площадь, за отопление которых нужно платить.

Но помните, что они входят в строку «квартплата».

Также следует помнить, что вы вносите плату за общедомовые нужды пропорционально метражу принадлежащей вам недвижимости.

Кстати, владельцам квартир с нестандартной планировкой следует помнить, что в площадь квартиры не входят ниши, высота которых менее 1,8 м; площадь под лестничным проемом (для двухуровневых квартир), если высота от пола до нижней части лестницы не превышает 1,6 м (измеряется по перпендикуляру к полу); место под функциональной печью или камином; дверные проемы, арочные проемы, если их ширина меньше 2 м.

Что касается балкона, то есть еще несколько важных моментов, которые следует учитывать. Вы можете распоряжаться только внутренней площадью балкона, внешняя часть является собственностью всех жильцов дома. В этом есть свои плюсы.

Чтобы оно могло переползать на другие балконы, его владелец должен заручиться согласием других владельцев балконов.

Калькулятор площади пола

Чтобы не мучиться с ручными расчетами на бумаге и не осваивать компьютерные программы, можно воспользоваться помощью онлайн-калькуляторов. Такую возможность предоставляет масса Интернет-ресурсов. В специальном окошке достаточно ввести все данные, и после нажатия кнопки «рассчитать» в новом поле или на новой странице откроются итоговые посчитанные данные. Обычно все показатели вводятся в метрах, но по желанию можно указать и другие единицы измерения.

У онлайн-калькуляторов есть свои плюсы и минусы

Достоинства онлайн калькуляторов:

• не нужно считать вручную;
• можно легко получить площадь любой фигуры;
• скорость расчетов и их точность высоки.

Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

• высота потолков;
• высота и ширина дверных проемов;
• высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

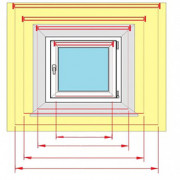
Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

1. Стена с дверью:
   • 2,5 м * 5,6 м = 14 м². — общая площадь длинной стены
   • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 м².
   • стена без учета дверного проема — 14 кв.м — 1,89 м² = 12,11 м²
2. Стена с окном:
   1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 м².
   2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 м², округляем, получаем 1,75 м².
   3. стена без оконного проема: 8 кв. м — 1,75 м² = 6,25 м².

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 м² + 12,11 м². + 8 м² + 6,25 м². = 40,36 м².

Основные понятия

Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

а

Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения

• квадратный миллиметр (мм2);
• квадратный сантиметр (см2);
• квадратный дециметр (дм2);
• квадратный метр (м2);
• квадратный километр (км2);
• гектар (га).

Метод Герона

Античный математик Герон Александрийский предложил свой способ получения квадратуры треугольника. Для вычислений достаточно знать длину трех его сторон, хотя сама методика достаточно сложна и не поддастся пятиклассникам:

1. Определите периметр: сложите отрезки сторон: a+b+c. Разделите число надвое. Полученные данные называются полупериметр (p) и имеют ключевое значение в геометрическом уравнении Герона.
2. Проведите вычисление по формуле: p (p — a) (p — b) (p — c). Т.е. сначала вычтите по отдельности длину каждой из сторон из значения полупериметра, а затем перемножьте между собой три полученных числа и сам полупериметр.
3. Извлеките корень из итогового значения. Искомая величина найдена.

Например, грани длиною 3, 4 и 5 см образуют полупериметр 6 см. После умножения согласно формуле получается значение 36. Корень из 36 равняется 6. Значит, 6 см2 — площадь этого треугольника. Для равносторонней фигуры расчет еще проще.

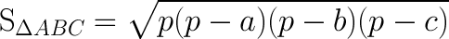
Теорема (формула площади треугольника)

Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

где  — сторона треугольника,  — проведенная к ней высота.

Доказательство:

 Пусть  — высота треугольника (рис. 148). Докажем, что 

Проведем через вершины  прямые, параллельные сторонам треугольника, и обозначим точку их пересечения  Таким образом, мы «достроили» треугольник  до параллелограмма  в котором отрезок  также является высотой, проведенной к стороне 

По формуле площади параллелограмма  Треугольники  равны по трем сторонам (у них сторона  общая,  как противолежащие стороны параллелограмма). Эти треугольники имеют равные площади. Тогда площадь треугольника  составляет половину площади параллелограмма 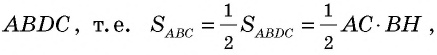 что и требовалось доказать. 

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов:

где  — катеты прямоугольного треугольника.

Действительно, в прямоугольном треугольнике высота, проведенная к катету, совпадает с другим катетом.

Следствие 2

Площадь ромба равна половине произведения его диагоналей:

где  — диагонали ромба.

Действительно, диагонали делят ромб на четыре равных прямоугольных треугольника с катетами  (рис. 149). Используя следствие 1, имеем:

Следствие 3

Площадь равностороннего треугольника со стороной  вычисляется по формуле

Обоснуйте это следствие самостоятельно.

Опорная задача

Медиана делит треугольник на два равновеликих треугольника. Докажите.

Решение:

Пусть  — медиана треугольника  (рис. 150).

Проведем высоту  треугольника  Этот отрезок является одновременно высотой треугольника  проведенной к стороне  и высотой треугольника  проведенной к стороне  Учитывая равенство отрезков  имеем:

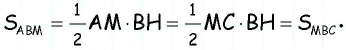
Эта задача имеет интересные обобщения: если высоты двух треугольников равны, то отношение площадей этих треугольников равно отношению их оснований; если основания двух треугольников равны, то отношение площадей этих треугольников равно отношению их высот.

Докажите эти утверждения самостоятельно.

Рекомендую подробно изучить предметы:

Геометрия Аналитическая геометрия Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

• Соотношения между сторонами и углами произвольного треугольника
• Окружность и круг
• Описанные и вписанные окружности
• Плоские и пространственные фигуры
• Взаимное расположения прямых на плоскости
• Треугольник
• Решение треугольников
• Треугольники и окружность

Расчет через окружности

В математике популярен также прием расчета, рассматриваемого в статье, значения через помещение фигуры в окружность или наоборот. Такая окружность называется описанной. Если она находится внутри, то она называется вписанной. Именно в этом разделе возникает большинство вопросов, как найти площадь равностороннего многоугольника с тремя углами.

Описанная окружность обязательно должна проходить через все вершины, вписанная должна проходить через стороны только в одной точке по касательной.

Чертеж равностороннего треугольника, описанного или вписанного в окружность

Если в условии задачи дан радиус вписанной и описанной окружности, то из них также можно составить выражение, так как вместе они дадут суммарную длину высоты. Как рассчитывается площадь при ее помощи, показано выше: h = R + r .

Преобразовав формулу ,  применив расчет высоты h = R + r,  можно получить следующее значение: . Данную формула можно упростить еще больше, ведь радиус описанной окружности можно выразить через радиус вписанной. Согласно свойствам этих окружностей R = 2r, где r — это радиус вписанной окружности, R — это радиус описанной. Соответственно площадь правильного треугольника будет высчитываться так: .

Если же будет дан размер радиуса описанной окружности, то выражение будет выглядеть следующим образом: .

Использование этих свойств пригодится для расчета стороны фигуры. Для того чтобы ее найти можно воспользоваться выражением  для описанной окружности, и   для вписанной.

Учитывая радиус описанной окружности можно найти искомое значение при помощи возведения стороны в куб, после чего результат делится на радиус, увеличенный в 4 раза. Математически его можно записать следующим образом: .

Процесс расчета, чему равен показатель площади равностороннего треугольника через любую из предложенных формул не должен вызывать особых затруднений. Для того чтобы успешно справиться с этой задачей не нужно запоминать все указанные способы, достаточно запомнить основные общие формулы расчета, а также свойства и признаки этой фигуры.

Внимание! Для проверки правильности расчетов можно воспользоваться несколькими способами, результаты должны совпасть. Площадь равностороннего треугольника

Площадь равностороннего треугольника

Площадь равностороннего треугольника, вписанного в окружность

Применив логическое мышление, расчеты с легкостью преобразовываются в частные случаи, коих гораздо больше. Нецелесообразно забивать голову большим количеством нерелевантной информации, лучше развивать причинно-следственную связь для преобразования выражений.

Площадь прямоугольного треугольника — формулы и калькуляторы

Прямоугольный треугольник — это треугольник, в котором один угол прямой (90°).

По основанию и высоте площадь прямоугольно треугольника равна половине произведения катетов треугольника.

Площадь прямоугольного треугольника по двум катетам — расчет:

Формула	Результат
S = ½ × a × b
	Катет a
Катет b

Площадь прямоугольного треугольника через гипотенузу и угол:

Формула	Результат
S = ¼ × c² × sin (2α)
	Сторона c
Угол α

Площадь прямоугольного треугольника через катет и угол — онлайн калькулятор:

Формула	Результат
S = ½ × b² × tg (α)
	Сторона b
Угол α

Если в треугольник вписана окружность и известны отрезки, на которые она делит гипотенузу, то площадь прямоугольно треугольника равна произведению этих отрезков.

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность:

Формула	Результат
S = d × e
	Отрезок d
Отрезок e

Площадь прямоугольного треугольника через гипотенузу и вписанную окружность — расчет:

Формула	Результат
S = r × (r + c)
	Сторона с
Радиус r

Площадь прямоугольно треугольника по трем сторонам (формула Герона) равна произведению разностей полупериметра треугольника и каждого из катетов. Полупериметр p = ½ × (a + b + c)

Площадь прямоугольного треугольника по формуле Герона:

Формула	Результат
S = ( ½ × (a + b + c) — a) × ( ½ × (a + b + c) — b)
	Сторона a
Сторона b
Сторона c

Формула площади для параллелограмма, ромба и трапеции

Параллелограмм, ромб и трапеция отличаются от квадрата и прямоугольника тем, что не все их углы имеют 90°. Из-за этого их площадь изменится, даже при равных значениях сторон, по отношению к площади квадрата и прямоугольника.

Параллелограмм является четырехугольником, чьи стороны попарно параллельны. Частными случаями данной фигуры являются прямоугольник, квадрат и ромб.

Площадь параллелограмма можно найти тремя способами:

• через сторону и высоту;
• через две стороны и величину угла между ними;
• через диагонали и угол между ними.

Ромб является частным случаем параллелограмма, чьи стороны равны.

Его площадь можно найти тремя способами:

• по длине стороны и высоте;
• по длине стороны и углу;
• по длинам его диагоналей.

Трапеция имеет четыре угла, которые не равны между собой, но в сумме дают 360°. Две стороны данной фигуры параллельны, а две другие — нет. Параллельные стороны считаются основаниями трапеции, непараллельные — боковыми сторонами.

Площадь трапеции можно найти двумя способами:

• по формуле Герона;
• по длине основ и высоте.

Помещение неправильной формы

Итак, рассмотрим на конкретных примерах способы вычисления метража:

1. Кухня. Каждая кухня имеет вентиляционную шахту, радиатор вдоль окна, дверь, окно и встроенную полку для хранения. Посчитаем чистую площадь стен кухни для поклейки обоев.

Данные кухни:

Высота =2,5 м;

Ширина=3 м;

Длина =3,5м.

Размер двери: ширина =0,8 м, высота = 2,0 м;

Размер окна: ширина 1,2 м, высота = 1,5м;

Вентиляционная шахта имеет следующие габариты: ширина =50 см, длина =30 см; высота = 2,5 м;

Габариты радиатора: ширина = 10 см, длина = 100 см, высота = 50 см.

Вычислим чистую площадь:

Сначала находим общую площадь: (3,5 м*2)+(3 м*2)*2,5 м = 32,5 м2;

Окна: S чистая = 1,2 м*1,5 м = 1,8 м2;

Двери: S чистая = 0,8 м*2,0 м = 1,6 м2;

Вентиляционная шахта: S чистая = (50 см * 2) + (30 см *2) *2,5 м = 400 см2 или 0,40 м2;

Встроенная полка: S чистая = (20 см*2) + (50 см * 2) *2,5 м = 350 см2 или 0,35 м2;

Площадь поверхности радиатора: (10 см *2) + (100 см *2) * 0,5 м = 110 см2 или 0, 11 м2.

Теперь определяем количество чистых квадратных метров, путем вычитания их общей площади: S чистая стен кухни = 32,5 м2 — 1,8 м2- 1,6 м2- 0,40 м2- 0,35 м2 — 0,11 м2 = 28,24 м2.

Полезный совет: для подсчета количества трубок обоев, необходимо разделить чистую площадь на количество листов в трубке.

Стандартная трубка имеет следующие размеры: ширина = 50 см, длина полотна = 10 м. Высота стен квартиры составляет 2,5 м, и этого следует, что в одну трубку обоев входит 4 бумажных полотна: 10 м /2,5 м= 4 листа.

Подсчитаем, сколько же нужно трубок, чтобы поклеить кухню:

28,24 м2 /4 = 7,06 трубок. Но так как, бумажное полотно может содержать рисунок с шагом 0,3 или 0,5, то следует округлить количество трубок до 8.

1. Ванная комната. Рассчитаем количество ящиков плитки для стандартной ванны. Чтобы правильно посчитать квадратуру помещения, необходимо производить измерения с учетом подрезки керамической плитки.

Нам известен стандартный размер двери: ширина =0,8 м; высота = 2,0 м.

Размер типовой ванной комнаты составляет: ширина 2,3 м; длина = 1,6 м, высота= 2,5 м.

Вычисляем чистую площадь ванны:

S ванны = (2,3 м*2) + (1,6 м*2) *2,5 м = 19,5 м2.

Затем, вычитаем следующие значения:

S чистая = 19,5 м2 — 1,6 м2 = 17,9 м2.

Для того, чтобы подсчитать, сколько же ящиков плитки Вам необходимо, следует определиться с размером керамического изделия. Плитка бывает следующих размеров: 10х10; 10х20; 20х30; 30х30. Возьмем более распространенный вариант: 30х30.

В одной упаковке находится 10 штук и, зная размер плитки, можно высчитать количества штук на 1 м2:

Определим, количество целых плиток и количество подрезки:

17,9 м2 / 9= 1,9 — округляем и получаем 20 коробок целых плиток;

20 * 7 = 140 маленьких плиток, размером 10х10.

Если класть плитку по плоскости без подрезки, то следует брать 20 ящиков, а если с подрезкой, то 16.

1. Балкон. Чтобы получить чистую площадь балкона, необходимо измерить рамы с остеклением. Периметр балкона вымеряется без учета окон.
2. Гараж. Как правило, гараж представляет собой коробку с маленьким окном. Для подсчета чистой площади, необходимо измерить размеры ворот.

Померить площадь круглого окна, перекрытия, стены здания в виде неправильной формы или восьмигранника, можно с помощью подручных средств.

Возьмите рулетку и вымеряйте максимальный диаметр круга, например, он получился 100 см. Вычисляем радиус: 100 см /2 =50 см — это ¼ круга в виде треугольника.

Если круг зрительно разделить на 4 части, и соединить точки прямыми линиями, мы получим 2 равнобедренных треугольника или 1 квадрат. Нам известна часть равнобедренного треугольника, следовательно, все стороны будут по 50 см. Остается найти площадь квадрата, где все стороны по 50 см. Вычислить общую площадь любой конструкции можно с помощью онлайн — программы.

Смотрите видео, в котором мастер подробно разъясняет, как правильно высчитать площадь стен в квартире:

Как определить площадь комнаты в квадратных метрах

Для чего нужно знать площадь помещения

Первая причина проведения замеров и соответствующих вычислений — покупка строительных и отделочных материалов. Площадь пола потребуется для приобретения ламината, линолеума, ковролина. Подготовительные работы в виде стяжки, установки лаг, выравнивания основания также потребуют знания квадратуры.

Для стен считают количество штукатурки, шпаклевки, обоев. Объем краски, грунтовки также рассчитывают по отношению к квадратному метру.

Причины для нахождения площади внутренних поверхностей:

• Проверить расчеты наемных работников. Часто они считают квадратуру всех отделочных работ на начальном этапе, когда на стенах нет выравнивающего слоя по маякам, чистовой шпаклевки. После проведения всех этих работ квадратура обоев и покраски значительной уменьшится.
• При закладывании проводки на освещение. Определяют количество светильников в соответствии с номами освещенности.
• Площадь важна при установке отопительных агрегатов, разводке радиаторных контуров. По показателям выбирают мощность приборов вентиляционной системы.

Часто приходится высчитывать площадь помещения?

Часто
62.5%

Редко
37.5%

Одни раз измерил и записал
0%

Проголосовало: 8

Формула площади для квадрата и прямоугольника

Геометрия, как часть математики, рассматривает целый ряд геометрических фигур: круг, квадрат, прямоугольник, треугольник и многих других.

Геометрические фигуры являются множеством точек на плоской поверхности, которые соединяются прямыми и на выходе становятся разными фигурами с разными особенностями.

Параметры геометрических фигур, такие как длины сторон, периметр, площадь, можно находить разными способами в зависимости от типа фигуры.

Площадь в геометрии обозначается знаком S, от английского square — площадь. Понятием площади пользуются как люди науки — математики, физики, так и люди рабочих профессий, например, строители.

Данная характеристика измеряется в единицах измерения в квадрате, например, квадратный сантиметр (см2), квадратный метр (м2), гектар (га).

Квадрат и прямоугольник являются фигурами, у которых есть по 4 прямых угла. Их отличает только длина сторон — у прямоугольника не все 4 стороны равны, они равны попарно относительно противоположных.

Площадь правильно построенного прямоугольника можно найти через перемножение его сторон друг на друга.

С помощью данной формулы можно найти площади классов или комнат, а также стен, что может помочь как в решении математических, так и бытовых задач.

3d моделью прямоугольника можно считать параллелепипед.

Площадь квадрата можно найти двумя способами:

• по длине стороны в квадрате;
• по длине диагонали.

Так как квадрат является частным случаем прямоугольника, его площадь также можно найти по формуле S=a×b, однако в таком случае a и b будут равны, а формула по смыслу будет повторять выше написанную.

В некоторых случаях необходимо нахождение площади квадрата через диагональ. Это может быть связано с решением определенной геометрической задачи или в связи с практическим удобством.

Считаем количество плитки

Зная площадь комнаты, рассчитать количество напольного покрытия будет несложно. Разберемся, как выяснить, сколько плитки понадобится для конкретной комнаты. Для этого нужно узнать, какова площадь одного элемента плиточного покрытия. Зная эти данные, легко произвести необходимые расчеты. Например:

• площадь комнаты – 15 м2;
• размер одной единицы плитки – 0,20х0,30 м.

Расчет количества плитки на пол

Таким образом, площадь одной плитки составит 0,2х0,3 = 0,06 м2. Далее общую площадь комнаты делим на площадь одной плитки и получаем: 15/0,06 = 250 единиц. Именно столько плиток потребуется, чтобы закрыть весь черновой пол в данном помещении. Точно таким же методом вычисляется и количество ламината или паркетной доски, а также других материалов.

Видео – Рассчитываем линолеум

Чтобы высчитать площадь пола в комнате, а затем – и расход материала, достаточно знать элементарные математические формулы и уметь пользоваться калькулятором. Имея последний под рукой (а сейчас калькулятор есть в каждом телефоне), произвести расчеты можно быстро. Главное – быть внимательными при снятии замеров.

Как рассчитать квадратные метры стен

Онлайн-калькулятор, который представлен практически на всех специализированных сайтах – это отличная возможность моментально рассчитать кв. метры поверхности стен. Высчитывать эту величину необходимо для того, чтобы правильно определить необходимое количество строительного материала.

Удобный онлайн-калькулятор дает возможность не только подсчитать количество квадратных метров, но и количество, например, обоев, которое необходимо для конкретной квартиры или комнаты.

Вообще, онлайн калькулятор является очень удобным инструментом для тех, кто не знает, как рассчитать кв. метры площади стен, однако, чтобы им воспользоваться, нужно правильно ввести все параметры:

Но если по какой-либо причине калькулятор в Интернет сети недоступен, то расчитать квадратуру комнаты и площадь стен в квадратных метрах придется вручную, по следующей формуле:

S – площадь стен (в кв.м)

Р – периметр комнаты (в метрах)

С – высота стен (в метрах).

Перед тем, как рассчитать квадратные метры стен, необходимо узнать периметр комнаты. В случае, если помещение – квадрат, то периметр считается легко: просто длина стены умножается на четыре, но в случае прямоугольника следует периметр комнат считается по формуле:

Р = (А + В) х 2, где:

Но перед тем, как высчитать квадратный метр стен, нужно рассчитать квадраты дверных и оконных проемов, если таковые есть. Это нужно для того, чтобы из общей площади стены в квадратных метрах вычесть площадь окон и дверей, чтобы не покупать лишний стройматериал.

При этом тем, кто интересуется, как рассчитать квадратуру комнаты, следует учесть, что квадраты комнат с выступами или же углублениями будут отличаться от аналогичного параметра комнат, форма которых квадрат или прямоугольник, не на один квадратный метр. Вот почему следует к полученной величине площади таких комнат добавлять каждый квадратный метр углубленного участка или выступа.

Площадь равностороннего треугольника по стороне

Пусть в равносторннем треугольнике известна сторона a (a=b=c) (Рис.1):

Найдем площадь треугольника. Поскольку в треугольнике напротив равных сторон расположенные равные углы (см. статью Соотношения между сторонами и углами треугольника), то в равносторннем треугольнике все углы равны. Но сумма всех углов треугольника равна 180°. Следовательно все три угла равностороннего треугольника равны 60°. Для треугольника ABH применим теорему синусов:

Учитывая, что , получим:

Площадь треугольника по основанию и высоте имеет следующий вид:

Подставляя (1) в (2), получим:

Пример 1. Сторона равностороннего треугольника равна a=5. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (3). Подставляя значение a=5 в (3), получим:

Ответ:

Площадь треугольника по трем сторонам

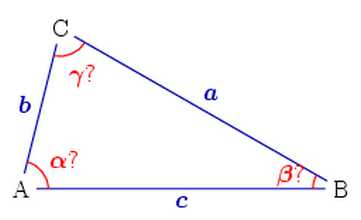Найти площадь треугольника можно различными способами. Конечно же, в зависимости от данных переменных и подбирается необходимая формула. В основном, для нахождения площади треугольника применяется формула Герона.

Если известны все три стороны треугольника ABC, то формула площади треугольника по трем сторонам легко применится на практике:

где:

• p – полупериметр треугольника,
• a, b, c – длины сторон треугольника.

Периметр – это сумма длин всех сторон треугольника. Соответственно полупериметр – это сумма длин всех сторон разделенная на 2.

abc

Также можно найти площадь треугольника и по другим формулам – через синус и косинус.