Квадратный метр: как правильно использовать эту единицу измерения

Как рассчитать площадь комнаты пошаговая инструкция

При расчете площади нужно знать длину, ширину и высоту комнаты

Можно, конечно, заглянуть в техническую документацию дома и посмотреть в ней все нужные характеристики. Но, во-первых, там нередко бывают ошибки, во-вторых, иногда проще вычислить всё самостоятельно, чем найти документы.

Для проведения подсчётов нам понадобятся определённые инструменты, большинство из которых можно запросто найти в каждом доме. А именно:

• рулетка;
• карандаш;
• бумага для записей;
• калькулятор (можно использовать калькулятор, который размещён на нашем сайте);
• трезвость ума и ясность мыслей.

Пол

Чтобы высчитать квадратуру пола в прямоугольной или квадратной комнате, необходимо узнать её длину и ширину.

Проводить замеры лучше у основания стен, а для этого желательно отодвинуть или вынести всю мебель. Но, если такая процедура в ваши планы не входила, можно мерить и по центру. Главное при этом, чтобы воображаемая линия, по которой будет производиться измерение, располагалась под углом в 90° к стене.

После того как данные замеров получены и проверены, их нужно перемножить по формуле , где S — площадь в квадратных метрах, a и b — длина и ширина, соответственно.

Если к основному помещению прилегает ниша или какое-нибудь другое — его площадь необходимо вычислить по тому же алгоритму, и результаты приплюсовать к площади комнаты. Если есть различные выступы, которые занимают его часть — их также следует измерить и полученный результат вычесть из общего.

С квадратами и прямоугольниками всё просто. А как посчитать S комнаты, если она имеет неправильную форму? Здесь придётся применить логическое мышление, и немного вспомнить школьный курс алгебры и геометрии. Но давайте по порядку.

Если помещение неправильной формы

Постарайтесь мысленно или на бумаге разделить комнату на простые элементы (квадраты, прямоугольники, треугольники). Далее, нужно будет высчитать размеры каждого из них, и результаты сложить.

• для треугольника — . Где a — длинна основания треугольника, b — высота, проведённая от вершины к основанию;
• для круга — . Где 3,14, r — радиус круга (чтобы узнать радиус — найдите с помощью рулетки самое длинное расстояние между стенами и разделите его на 2);
• для полукруга — (буквенные обозначения совпадают с предыдущим пунктом).

Как оказалось, и в таком случае ничего сложного нет. Главное, тщательно проверять результаты замеров, чтобы в расчёты не закралась случайная ошибка, и их не пришлось производить заново.

И ещё. Если вы хотите произвести монтаж тёплого пола, не забудьте отдельно вычислить площадь, которую занимает мебель, и вычтите её из общего значения для помещения.

С полом мы разобрались. Но при подготовке, допустим, к переклеиванию обоев это вам мало чем поможет. Нужно будет узнать точное количество квадратных метров, которое занимают  стены.

Стены

Площадь каждой отдельно взятой стены можно высчитать так же, как и квадратуру пола. Только теперь вместо ширины помещения нужно будет измерить её высоту. Множим длину стены на высоту и получаем необходимый нам результат в квадратных метрах.

Измерение высоты лазерной рулеткой

А можно вычислить и для всех стен сразу. Для этого вам понадобится узнать периметр пространства. Возьмите рулетку и измерьте длину каждой стены, результаты сложите — это и будет периметр. Остаётся измерить высоту комнаты и воспользоваться следующей формулой: , где p — периметр, а h — высота.

Теперь необходимо разобраться с оконными, дверными и прочими проёмами, присутствующими в помещении.

Точнее, рассчитать площадь каждого из них (по формулам, представленным выше, в зависимости от формы проёма), результаты суммировать и вычесть из общего количества.

Существует также ряд общих рекомендаций по проведению замеров.

Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

• высота потолков;
• высота и ширина дверных проемов;
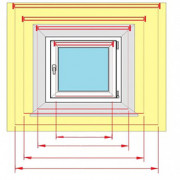
• высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

1. Стена с дверью:
   • 2,5 м * 5,6 м = 14 м². — общая площадь длинной стены
   • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 м².
   • стена без учета дверного проема — 14 кв.м — 1,89 м² = 12,11 м²
2. Стена с окном:
   1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 м².
   2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 м², округляем, получаем 1,75 м².
   3. стена без оконного проема: 8 кв. м — 1,75 м² = 6,25 м².

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 м² + 12,11 м². + 8 м² + 6,25 м². = 40,36 м².

Особенности расчета площади простых стен и стен, содержащих выступы и ниши

Теперь давайте рассмотрим такой важный момент, как расчет площади стен комнаты. Зная именно эту величину, вы сможете купить нужное количество обоев для ремонта. В этом нет ничего сложного: измерьте длину, ширину и высоту помещения.

Далее площадь стен высчитываем по формуле:

Sстен = Р х С, где Р – периметр комнаты, С – высота стен.

Периметр комнаты считаем по формуле:

Р = (А + В) х 2, где A – длина, B – ширина.

Для получения более точных результатов, из общей площади стен необходимо вычесть площадь дверных и оконных проемов.

Площадь стен комнаты с выступами или углублениями будет отличаться от площади стен простой комнаты. Не забудьте к основному значению прибавить площадь стены выступающего или углубленного участка.

Будьте внимательны, производя измерения и расчеты. Если вы используете лазерную рулетку, то следите за тем, чтобы луч был направлен строго перпендикулярно стене, иначе вы получите большую погрешность в результатах.

Стены комнаты с выступами. Фото — gohawaii.about.com

Начиная ремонт, первым делом нужно определить необходимое количество строительных материалов. Провести расчеты могут специалисты, которые будут выполнять работы. Но они часто делают вычисления с большой погрешностью в свою пользу. Рассмотрим, как самостоятельно посчитать площадь стен.

Основание трапеции

Рассмотрим, как правильно рассчитать площадь трапеции. Трапеция представляет собой четырехсторонний многоугольник с одной парой параллельных сторон. Если две непараллельные стороны имеют одинаковую длину, форма называется равнобедренной или обычной трапецией. Если непараллельные стороны имеют разную длину, она называется неравнобедренной. Однако, несмотря на эту дополнительную сложность в определении, площадь неправильной трапеции может быть рассчитана с помощью простой формулы.

Измерения для расчета площади трапеции:

1. Выровнять прямой край транспортира вдоль более короткой из двух параллельных сторон.
2. Использовать транспортир, чтобы провести линию перпендикулярно от основания трапеции вплоть до противоположной параллельной стороны.
3. Измерить расстояние высоты с помощью линейки.
4. Измерить длину более короткой параллельной стороны.
5. Измерить длину более длинной параллельной стороны.
6. Чтобы найти площадь трапеции, предварительно нужно вычислить среднюю величину двух ее параллельных сторон: (a+b)/2.
7. Площадь равнобедренной (или любой) трапеции равна произведению средней длины основания и вершины на высоту.
8. Площадь трапеции: S=1/2×h×(a + b).

Нужно обратить внимание, что высота трапеции всегда перпендикулярна основанию, точно так же, как высота параллелограмма. Пример: a=3 см, b=5 см, h=4 см

S=4х(3+5)/2=16.

Ответ: 16 см2.

Измерение площади ромба

Ромб — особый вид параллелограмма, имеющий равные стороны и равные противоположные углы. Площадь ромба можно определить, используя три способа.

1. Метод высоты основания. Сначала выберите одну любую сторону в качестве базы, так как они имеют одинаковую длину. Затем определите высоту — перпендикулярное расстояние от выбранного основания до противоположной стороны.

Площадь является произведением этих двух величин и определяется по формуле: S=a×h, где: S – площадь ромба, h — высота ромба, AB=BC=AD=DC=a – сторона ромба.

2. Метод диагоналей. Другая простая формула для площади ромба, когда известны длины диагоналей. Площадь составляет половину произведения диагоналей.

В качестве формулы: S=1/2xACxBD, где: S – площадь ромба, AC– большая диагональ, BD — меньшая диагональ.

3. Использование тригонометрии. В тригонометрии, есть удобная формула, когда известны длина стороны и любой угол:

S=a2×sin α, где: S – площадь ромба, B=BC=AD=DC= a – сторона ромба, α — острый угол, β — тупой угол.

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту

Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный

Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка

Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Предремонтные замеры пола

Как рассчитать площадь пола перед проведением ремонтных работ, например, замены линолеума или покраски? Для квадратного или прямоугольного помещения сначала нужно будет измерить длину и ширину комнаты. Затем умножить длину и ширину, получим длина x ширина = площадь. Таким образом, если комната имеет размеры 3 метра в ширину и 5 метров в длину, общая площадь составит 15 квадратных метров.

Это измерение можно использовать при расчете необходимого количества плиточного раствора, герметика, линолеума, которые владелец планирует использовать для своего проекта. Чтобы рассчитать площадь для подбора материалов, как правило, нужно добавить 10% коэффициент запаса: просто умножьте площадь на 1,1, а затем округлите до целого значения.

В примере, когда общая площадь составляет 15 м2, нужно будет заказать дополнительное количество плитки и раствора для 16,5 квадратных метра. Если комната не прямоугольная, нужно разделить ее на две или более элементарных геометрических фигур, чтобы рассчитать общую площадь.

Обозначение площади

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Если параметры фигуры переданы в разных единицах длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Круг — это когда множество точек на плоскости удалены от центра на равном радиусу расстоянии. Радиусом принято называть прямую линию, соединяющую центр с любой точкой окружности.

1. S = π * r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

2. S = d 2 : 4 * π, где d — это диаметр.

3. S = L 2 ​ : 4 * π, где L — это длина окружности.

Формула нахождения площади в математике

Существует множество формул нахождения площади простых геометрических фигур, которые зависят, в основном, от количества углов, сторон и их соотношений.

Площадь прямоугольника

Прямоугольником является геометрическая фигура, все углы которой равны 90°. При этом таких углов должно быть, как минимум три, а четвертый будет равен 90° в силу закона о сумме углов четырехугольника в евклидовой геометрии.

Площадь квадрата

Квадратом является прямоугольник с равными сторонами. Все его углы равны 90°. Площадь квадрата можно найти сразу двумя способами:

• по длине стороны;
• через его диагонали.

По длине стороны:

Через диагонали:

Площадь круга

Кругом является часть плоскости, которая лежит внутри окружности. Круг не имеет ни одного угла, а точки его окружности находятся на равном удалении от центра.

Площадь круга можно найти двумя способами:

• через его радиус;
• через его диаметр.

Через радиус:

Радиус, упоминаемый в формуле, является линией или отрезком, соединяющим центр и любую из точек окружности.

Через диаметр:

Диаметр является отрезком, соединяющим две точки окружности и проходящим через центр. Он включает в себя два противоположно направленных радиуса.

Площадь эллипса

Эллипс является частным случаем окружности. Он, так же, как и круг, не имеет ни одного угла, но при этом точки окружности находятся на разном удалении от центра.

Найти площадь эллипса можно только одним способом: через произведение длин большой и малой полуосей эллипса и числа пи.

Площадь параллелограмма

Параллелограмм является геометрической фигурой с 4 углами и 4 сторонами, однако он отличается от прямоугольника по строению. Его противолежащие стороны попарно параллельны, а углы равны зеркально противолежащим.

Частными случаями параллелограмма являются квадрат, прямоугольник и ромб.

Найти площадь параллелограмма можно тремя способами:

• через сторону и высоту;
• через две его стороны и величину угла между ними;
• через диагонали и угол между ними.

Через сторону и высоту:

Через две стороны и величину угла между ними:

Через диагонали и угол между ними:

Площадь ромба

Площадь ромба также можно найти тремя способами:

• по длине стороны и высоте;
• по длине стороны и углу;
• по длине его диагоналей.

По длине стороны и высоте:

По длине стороны и углу:

По длине его диагоналей:

Площадь трапеции

Трапеция отличается от всех предыдущих фигур тем, что только две ее стороны, боковые, могут быть равны между собой. При этом они не параллельны. Две другие стороны параллельны, но не равны. Сумма углов трапеции равна 360°.

Площадь трапеции можно найти двумя способами:

• по формуле Герона;
• по длине основ и высоте.

По формуле Герона:

По длине основ и высоте:

Площадь треугольника

Треугольник является геометрической фигурой с тремя сторонами и суммой углов, равной 180°. По величине углов треугольники делятся на острые, тупые и прямоугольные. По числу равных сторон треугольники делятся на разносторонние, равносторонние и равнобедренные.

Площадь треугольника можно найти множеством способов:

• по гипотенузе и острому углу;
• через сторону и высоту;
• через три стороны;
• через две стороны и угол между ними;
• через три стороны и радиус описанной окружности;
• через три стороны и радиус вписанной окружности.

По гипотенузе и острому углу:

Через сторону и высоту:

Через три стороны:

Через две стороны и угол между ними:

Через три стороны и радиус описанной окружности:

Через три стороны и радиус вписанной окружности:

Почему не все так просто

Так вопрос, как рассчитать площадь любой поверхности может показаться смешным, ведь все мы учились в школе. Но не будем столь категоричными. Во-первых, со школьной скамьи многие из нас сошли со школьной скамьи очень давно. Во-вторых, не каждый раз в повседневной жизни приходится сталкиваться с необходимостью геометрических расчётов. И кое-что уже позабыто.

Ну и в третьих далеко не всегда поверхность имеет правильную форму. Тогда приходится изворачиваться, применяя более сложные приёмы расчёта. Это с квадратами и прямоугольниками все просто, но как быть в случае трапеции, треугольника и прочих сложных геометрических фигур?

Простой расчет прямоугольника

Если внимательно посмотреть вокруг, можно увидеть множество примеров прямоугольников. По определению, прямоугольник представляет собой четырехсторонний многоугольник, углы которой находятся под прямым углом, равным 90 градусам. Рассчитать площадь поверхности тела прямоугольника — простая математическая операция, которая наиболее часто применяется человеком в повседневной жизни

Почему важно знать формулу площади? Многие предметы и обстановка, окружающие человека, имеют прямоугольную форму: дом, стены, пол, крыша. И очень часто надо знать их площадь для строительства или ремонта

Если прямоугольник имеет длину b и ширину h, мы можем найти площадь S, умножив ширину на его длину. Следовательно: S=bxh.

Пример. Как рассчитать площадь прямоугольника, если известны сторона и ширина, например, длина 4 см и ширина 3 см, тогда: S=4х3=12.

Ответ: 12 см2.

Квадрат — разновидность прямоугольника с равными углами и сторонами.

S=bxb=b2.

Пример. Если квадрат имеет стороны 3 см, мы можем найти S, возведя в квадрат значение стороны. Следовательно, имеем: S=3х3=9.

Ответ: 9 см2.

Немного теории

Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.

Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний

Что такое 1 см² и 1 м²

Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.

Что такое один квадратный сантиметр

Один квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр. Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м².  В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².

Формулы

Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.

При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата

Надо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.

1. Имеем прямоугольник со сторонами 80 см и 50 см. Перемножаем эти цифры: 80 * 50 = 4000 см². Это и будет его площадь.
2. Стороны 322 см и 300 см. Получим: 322*300 = 96000 см².
3. Есть квадрат со стороной 60 см. Его площадь — 60 * 60 = 3600 см².

В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.

Простейший калкулятор для расчета площади прямоугольной комнаты.

Перевод квадратных сантиметров в квадратные метры

Когда имеем дело с сотнями сантиметров, удобнее и проще считать в метрах. Мы знаем, что в одном метре сто сантиметров. Давайте решим те же примеры, но переведем сантиметры в метры:

1. 80 см = 0,8 м; 50 см = 0,5 м. Перемножаем 0,8*0,5 = 0,4 м². То есть, 0,4 квадратных метра.
2. 322 см это 3,22 м; 300 см это 3 м. Теперь умножаем полученные цифры: 3,22 * 3 = 9,6 м².
3. 60 см равны 0,6 м. Площадь квадрата с такой стороной 0,6*0,6 = 0,36 м².

Цифры получаются намного меньше, запомнить их проще. И если мы хотим посчитать площадь комнаты в квадратных метрах, ее размеры мы меряем в метрах, а не сантиметрах. Можно перевести квадратные сантиметры в квадратные метры. Как уже говорили, в одном квадратном метре содержится десять тысяч квадратных сантиметров.

Соотношение квадратных сантиметров и квадратных метров

Если же у вас есть площадь в квадратных сантиметрах, чтобы перевести ее в квадратные метры, цифру надо разделить на 10 000. Например:

• 4000 см² / 10000 = 0,4 м²;
• 96000 см² / 10000 = 9,6 м²;
• 3600 см²/ 10000 = 0,36 м².

Как видите, все просто. Надо только запомнить основные положения и посчитать площадь комнаты в квадратных метрах будет совсем несложно. Нужно будет предварительно провести измерения, а потом заняться расчетами.

Единицы измерения

Применяются системные и внесистемные единицы измерения. Системные единицы относятся к СИ (Система Интернациональная). Это квадратный метр (кв. метр, м²) и единицы, производные от него: мм², см², км².

В квадратных миллиметрах (мм²), например, измеряют площадь сечения проводов в электротехнике, в квадратных сантиметрах (см²) — сечения балки в строительной механике, в квадратных метрах (м²) — квартиры или дома, в квадратных километрах (км²) — территории в географии.

Однако иногда используются и внесистемные единицы измерения, такие, как: сотка, ар (а), гектар (га) и акр (ас). Приведём следующие соотношения:

• 1 сотка=1 а=100 м²=0,01 га;
• 1 га=100 а=100 соток=10000 м²=0,01 км²=2,471 ас;
• 1 ас= 4046.856 м²=40,47 а=40,47 соток=0,405 га.

Для оценки сметы и объема закупок перед началом отделочных работ нужно знать метраж стен. Расход большинства строительных материалов (краски, штукатурки, шпаклевки) определяется площадью. Также этот параметр важен при поиске бригад, так как большинство отделочников работы оценивают по стоимости за квадратный метр.