Построение линии пересечения конусов методом концентрических сфер

Содержание:

Построение развёртки конуса
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Обобщения и замечания[править]
Габариты и видовые составляющие конуса Морзе
Основные сведения о хвостовиках и их обозначение
Усеченный геометрический объект
Усеченный геометрический объект
Развертка наклонного конуса
- Перенос линии с поверхности конуса на развертку
Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:
Особенности конструкции и основные типы конусов Морзе
Калькуляторы расчета размеров развертки конуса — с пояснениями
- - Несколько слов о рассчитываемых параметрах
  - Шаг 3 – определение величины центрального угла f
Как сделать елку из конуса своими руками
Как сделать конус из железа. Расчет развертки усеченного конуса из листового металла
- - Расчет заготовки выкройки для усеченного конуса
Услуги вальцовки недорого

Построение развёртки конуса

Конус

Развёртка конуса может быть выполнена двумя способами. (См. чертёж)

Если известен размер стороны конуса, из точки O
, циркулем чертится дуга, радиусом равным стороне конуса. На дуге откладываются две точки (A 1
и B 1
О
.
Строится конус в натуральную величину, из точки O
, в точку A
, ставится циркуль, и проводится дуга, проходящая через точки A
и B
. На дуге откладываются две точки (A 1
и B 1
), на расстоянии равном длине окружности и соединяются с точкой О
.

Для удобства, от можно откладывать половину длинны окружности, в обе стороны от осевой линии конуса.
Конус со смещёной вершиной строиться так же, как усечённый конус со смещёнными основаниями.

Построить окружность основания конуса в виде сверху, в натуральную величину. Разделить окружность на 12 или более равных частей, и отложить их на прямой поочерёдно.

Конус с прямоугольным (многогранным) основанием.

Конуса с многогранным основанием

В случае, если конус имеет ровное, радиальное, основание: (При построении окружности на виде с верху, путём установки циркуля в центр, и очерчивания окружности по произвольной вершине — все вершины основания укладываются на дугу окружности.
) Построить конус, по аналогии с развёрткой обычного конуса (основание строить по окружности, от вида сверху). Отложить дугу из точки O
. В произвольной части дуги поставить точку A 1
, и поочерёдно отложить все грани основания на дугу. Конечная точка последней грани будет B 1
.
Во всех иных случаях конус строится по принципу триангуляции (см. далее
).

Усечённый конус с доступной вершиной

Усечённый конус

Построить усечённый конус ABCD
в натуральную величину (См. чертёж).
Стороны AD
и BC
продожить, до появления точки пересечения O
. Из точки пересечения O
, провести дуги, с радиусом OB
и OC
.
На дуге OC
, отложить длину окружности DC
. На дуге OB
, отложить длину окружности AB
. Полученные точки соединить отрезками L 1
и L 2
.
Для удобства, от можно откладывать половину длинны окружности, в обе стороны от осевой линии конуса.

Как отложить длину окружности на дуге:

При помощи нитки, длина которой равна длине окружности.
При помощи металической линейки, которую следует изогнуть «по дуге», и поставить соответствующие риски.

Примечание:
Совсем не обязательно, что отрезки L 1
и L 2
, если их продолжить, будут сходится в точке O
. Если быть до конца честным, то сойтись они должны, но с учётом поправок на погрешности инструмента, материала и глазомера — точка пересечения может оказаться чуть ниже или выше вершины, что не является ошибкой.

Усечённый конус с переходом с круга на квадрат

Конус с переходом с круга на квадрат

Подготовка:

Построить усечённый конус ABCD
в натуральную величину (см. чертёж), построить вид сверху ABB 1 A 1
. Окружность поделить на равные части (в приведённом примере показано деление одной четверти). Точки AA 1 -AA 4
соединить отрезками с точкой A
. Провести ось O
, из центра которой провести перпендикуляр O-O 1
, высотой равной высоте конуса.
Ниже, первичные размеры снимаются с вида сверху.Построение:

Снять размер AD
и построить произвольную вертикаль AA 0 -AA 1
. Снять размер AA 0 -A
, и поставить «примерную точку», сделав отмашку циркулем. Снять размер A-AA 1
, и на оси O
, из точки O
O 1
AA 1
, до предполагаемой точки A
. Соединить отрезками точки AA 0 -A-AA 1
.
Снять размер AA 1 -AA 2
, из точки AA 1
поставить «примерную точку», сделав отмашку циркулем. Снять размер A-AA 2
, и на оси O
, из точки O
, отложить отрезок, снять размер из полученной точки до точки O 1
. Сделать отмашку циркулем из точки A
, до предполагаемой точки AA 2
. Провести отрезок A-AA 2
. Повторить, пока не будет отложен отрезок A-AA 4
.
Снять размер A-AA 5
, из точки A
поставить «примерную точку» AA 5
. Снять размер AA 4 -AA 5
, и на оси O
, из точки O
, отложить отрезок, снять размер из полученной точки до точки O 1
. Сделать отмашку циркулем из точки AA 4
, до предполагаемой точки AA 5
. Провести отрезок AA 4 -AA 5
.

Подобным образом построить остальные сегменты.Примечание:
Если конус имеет доступную вершину, и КВАДРАТНОЕ
основание — то построение можно провести по принципу усечённого конуса с доступной вершиной
, а основание — конуса с прямоугольным (многогранным) основанием
. Точность будет ниже, но построение существенно проще.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Линии сверху, линии снизу: как разобраться в символах на духовке

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения. Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Обобщения и замечания[править]

Используя вышеприведённую технику, можно построить развёртку практически любого объекта со сложной топографией.
При этом следует иметь в виду, что при работе с металлом следует брать внутренние размеры детали, т.к. при гибке и/или закатке, внешняя поверхность металла тянется, а внутренняя остаётся неизменной. (Верно при использовании современного гибочного оборудования. На устаревшем оборудовании, следует вводить поправки на износ поверхностей, и точность работы станка.)
При работе с металлом, толщиной свыше 3 мм, в зависимости от типа, марки металла и используемого гибочного оборудования — размеры следует брать не по внутренней стороне, а по «средней линии», которая проходит на половине толщины металла. Либо считать места сгибов не как прямые углы, а как дуги.
При изготовлении из металла, линии разметки (прямые, а не вспомогательные диагонали) могут использоваться как линии гиба, с последующей доводкой контура молотком/киянкой на вспомогательной поверхности.

Самодельные ножи из аустенитной нержавейки методом холодной ковки

Габариты и видовые составляющие конуса Морзе

Как делают парящие линии на натяжном потолке

В действительности существуют разные виды и размеры госта морзе-конусов, и они имеют неоднозначные названия в специальной литературе. Но их отличительной особенностью является их узнаваемость во всех культурах под определенными номерными знаками: 10, 100, 1000. При этом зандры-конусы меньшего размера 0.001″ и 0.0001″ в разговорной речи часто используют под американским термином: «зу» и «тенф».

Лучший способ измерения конуса – использовать калибровку, ибо на зандре имеются риски. Но для большой точности измерения используют таблицу пересчета размеров вплоть до сотой доли миллиметра. Таким образом, для того чтобы с точностью до миллиметра определять какой конус Морзе лучше всего использовать в данной ситуации, следует обращаться к таблице измерения диаметра изделия.

Кроме того, все инструментальные предметы с конусом Морзе в наше время имеют следующий стандарт ГОСТ 25557-82. Именно данная модель ГОСТ имеет сегодня наибольшую популярность в России по сравнению с предыдущими моделями. Имеется усовершенствованный способ удержания патрона и крепления.

Американские конусы различаются посредством дюймовой системы измерения, поэтому для лучшего понимания российским потребителем все метрические данные конуса переводятся в миллиметровую систему.

Видео: изготовление переходного конуса для сверлильного патрона под морзе 2.

Основные сведения о хвостовиках и их обозначение

Существует несколько видов исполнения инструментального конуса. Он может содержать резьбу, лапку или обходиться без них.

В его торце может быть нарезана резьба, которую делают для закрепления инструмента на шпинделе с использованием штревеля. Это специальный шток, предотвращающий выпадение инструмента. Также с его помощью изделие можно извлечь, если его случайным образом заклинит в шпинделе.

Если хвостовик изготовлен с лапкой, то она удерживает инструмент в шпинделе за счет того, что закреплена в специальном пазу. Лапка имеет два предназначения, с ее помощью легче достать изделие из шпинделя, а также создается жесткая фиксация и не будет проворачивания.

Также можно встретить исполнение с несколькими канавками и отверстиями. Они имеют разную глубину и размеры. Их задача – подводить к режущему инструменту смазочно-охлаждающую жидкость.

Хвостовики инструмента бывают различной конструкции и обозначаются буквенным кодом. Ниже приведена их расшифровка:

BI – внутренний, имеется паз;
ВЕ – наружный, имеется лапка;
AI – внутренний, имеется отверстие по оси;
АЕ – наружный, имеется отверстие по оси с резьбой;
BIK – внутренний, имеются паз и отверстие для подачи смазочно-охлаждающей жидкости (СОЖ);
ВЕК – наружный, имеется лапка и отверстие для подачи СОЖ;
AIK – внутренний, содержит отверстия по оси и для подачи СОЖ;
АЕК – наружный, содержит отверстие по оси с резьбой и отверстие для подачи СОЖ.

Наружный и внутренний соответствуют своим названиям. В зависимости от используемого инструмента, следует выбирать исполнение наружное или внутреннее.

Усеченный геометрический объект

Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.

Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.

Способы построения

Можно выделить два основных способа построения усеченного круглого геометрического объекта:

из круглого прямого конуса;
с помощью трапеции.

В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной

Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.

Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.

Площадь поверхности

Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:

Разрезать ее вдоль образующей и развернуть на плоскости.
Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую

В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).

Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:

S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).

Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.

Формула объема

Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:

V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).

Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:

V = 1/3*pi*h*(r12 + r22 + r1*r2).

Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:

V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).

Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.

Усеченный геометрический объект

Способы построения

Можно выделить два основных способа построения усеченного круглого геометрического объекта:

из круглого прямого конуса;
с помощью трапеции.

Площадь поверхности

В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).

Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:

S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).

Формула объема

V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).

V = 1/3*pi*h*(r12 + r22 + r1*r2).

Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:

V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S. Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5.
Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’1, 16=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
Соединяем точки A, B, C плавной линией.

Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:

Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

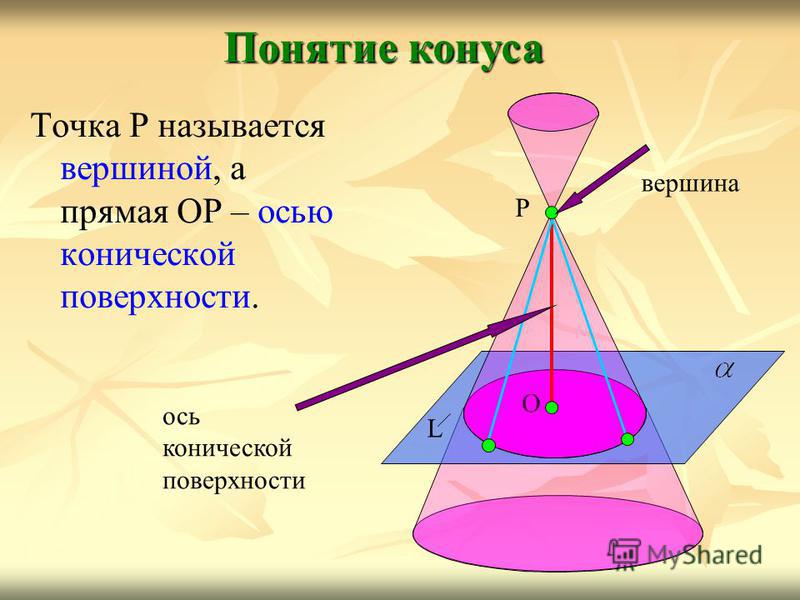
Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности

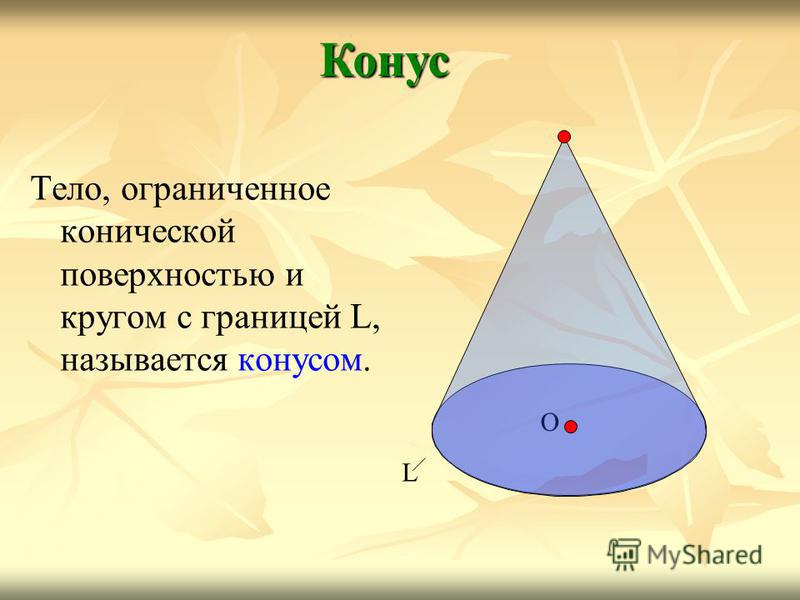
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L

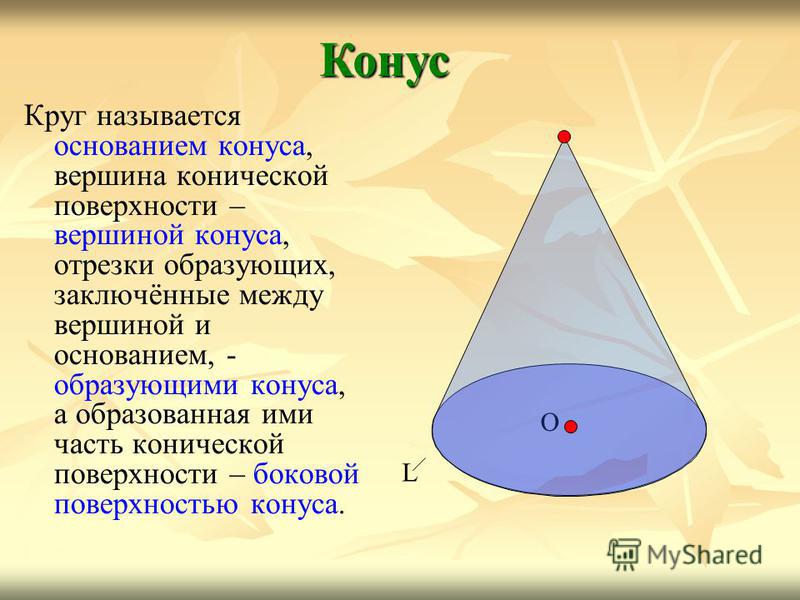
Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L

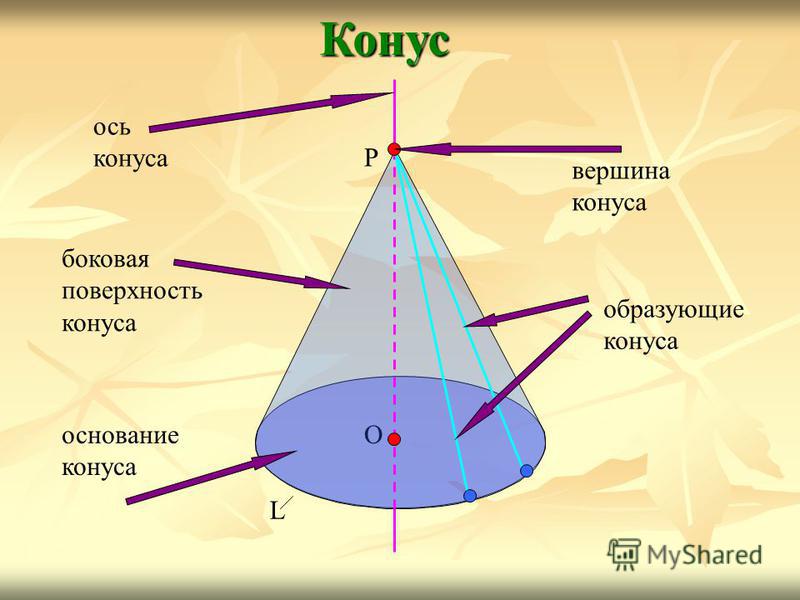
Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса

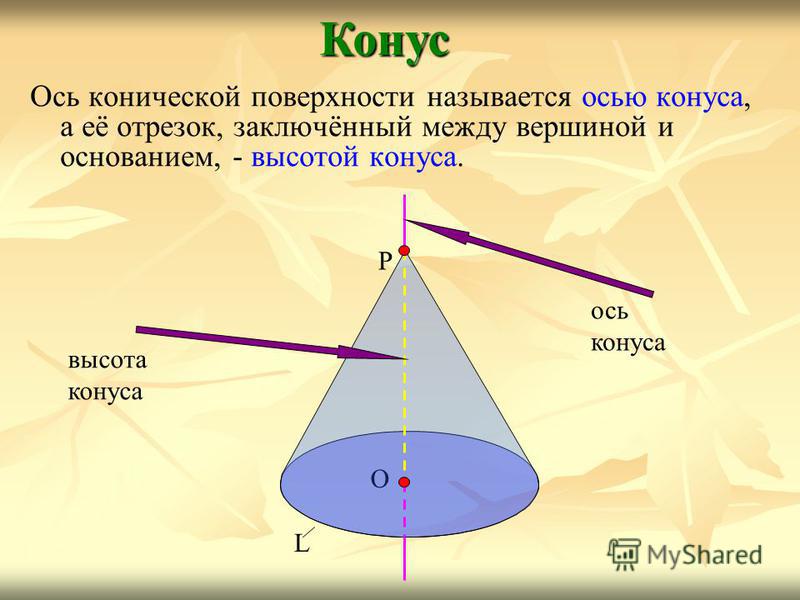
Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

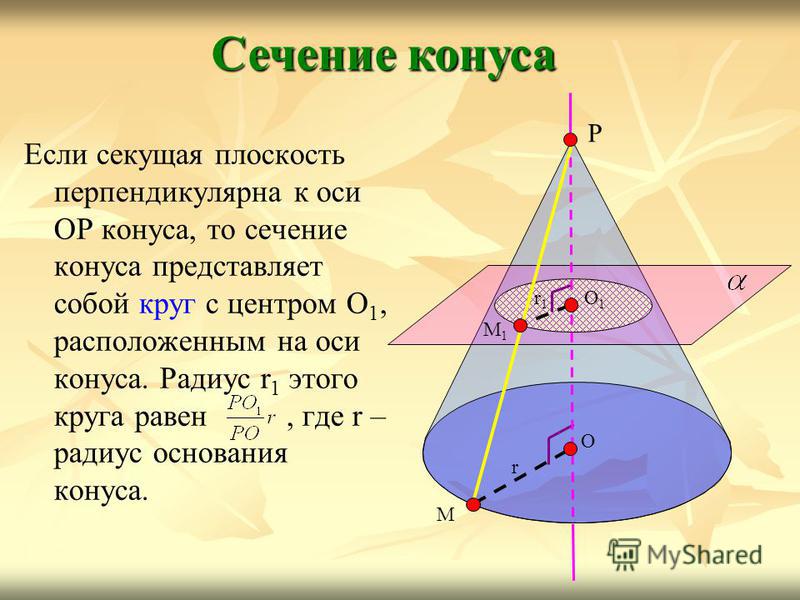
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1

Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

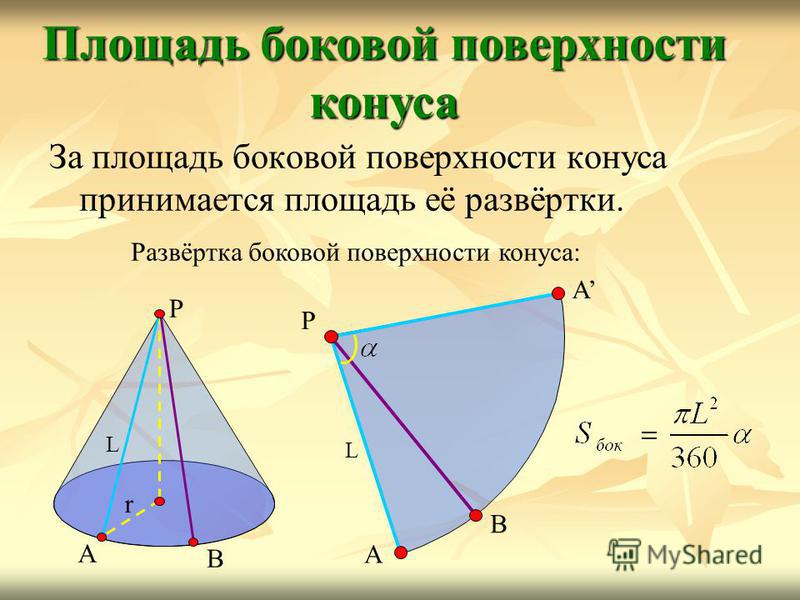
За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r

Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

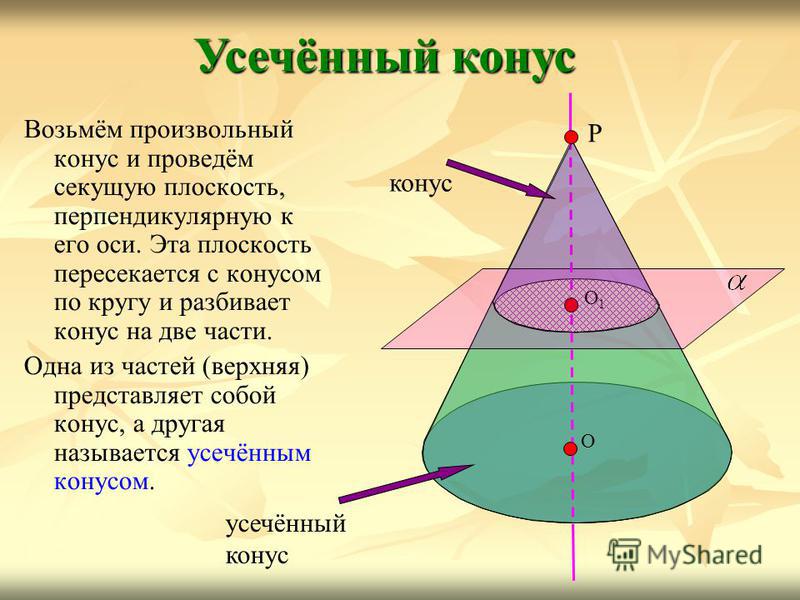
Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус

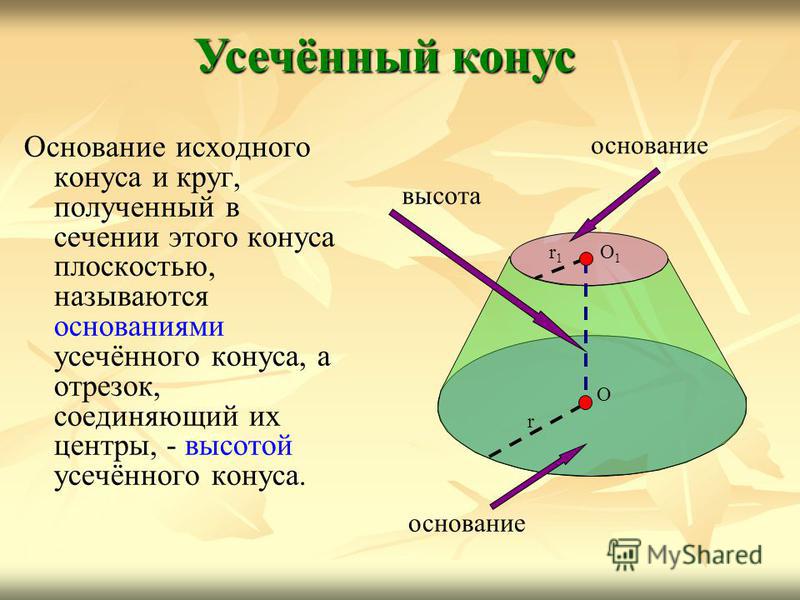
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота

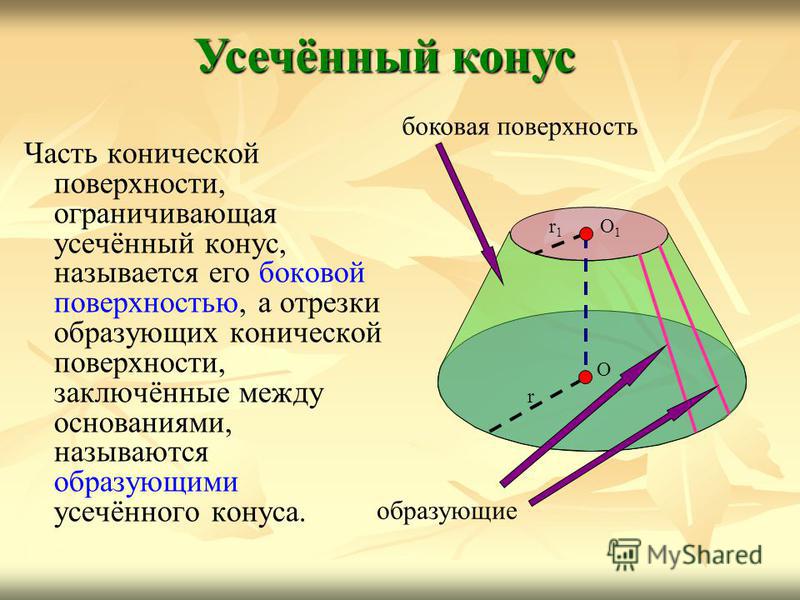
Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие

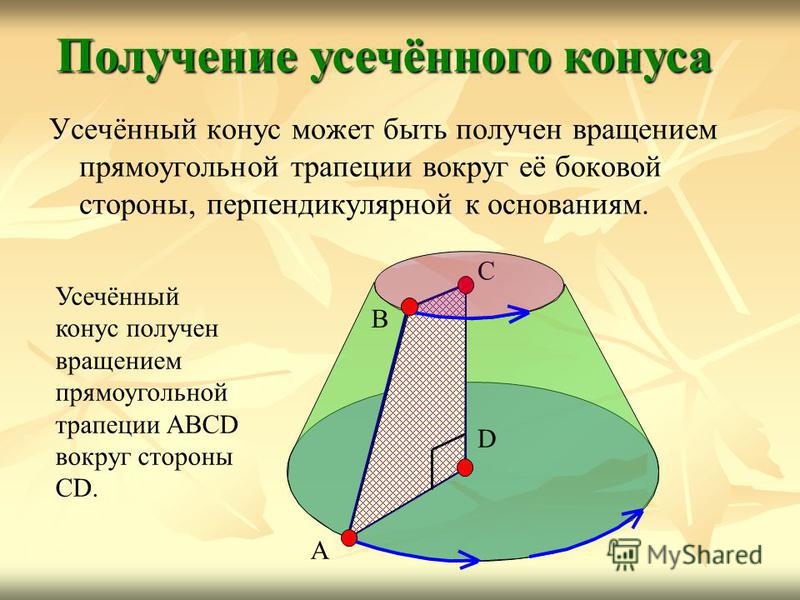
Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.

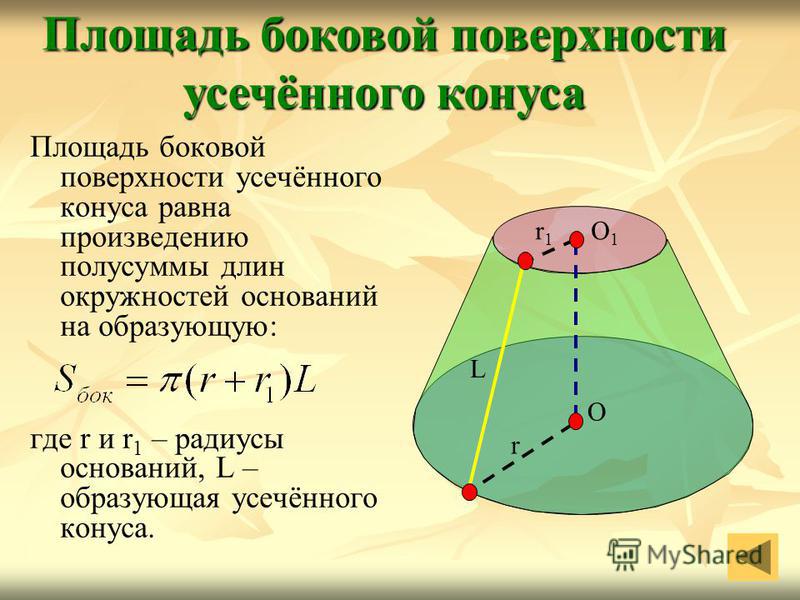
Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L

Особенности конструкции и основные типы конусов Морзе

Есть версия, что коническая конструкция появилась в результате постепенной эволюции токарного, фрезерного и сверлильного инструмента в результате изучения влияния износа инструмента на его характеристики и качество выпускаемых деталей. Было замечено, что в процессе работы инструмент с цилиндрическим хвостовиком изнашивался и начинал проворачиваться в кулачках, возникали биения и отклонения инструмента.

В процессе развития технологий машиностроения появился так называемый метрический конус, который отличается от своих предшественников постоянной конусностью и угловыми размерами. Его конусность составляет 1:20, уклон – 1°51’56”, а угол – 1°51’51”, тогда как до этого конусность была переменной и варьировалась от 1:19,002 до 1:20,047.

Согласно классификации, принятой в ГОСТах СССР конусы Морзе принято разделять на малые, большие и общего применения.

Исходя из особенностей конструкции, на сегодняшний день различают три типа конусов Морзе:

Гладкий;
С резьбой;
С лапкой.

Выпадение инструмента из шпинделя предотвращается самой конической формой хвостовика и отверстия в шпинделе или оправке. Дополнительно крепление хвостовика с лапкой в шпинделе происходит за счет вхождения лапки в специальный паз, резьбового – за счет резьбы в торце хвостовика.

Так же изготавливают инструмент с дополнительными пазами и отверстиями для подведения СОЖ. Это наиболее актуально для современных станков с ЧПУ.

Калькуляторы расчета размеров развертки конуса — с пояснениями

Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

(Если она уже известна – шаг пропускается)

Перейти к расчётам

Шаг 3 – определение величины центрального угла f

Перейти к расчётам

* * * * * * *

Итак, все данные имеются. Остается на листе бумаги циркулем провести две дуги рассчитанных радиусов. А затем из точки центра с помощью транспортира прочертить два луча под рассчитанным углом – они ограничат развертку по угловой длине.

Существуют и чисто геометрические методы построения довольно точной развертки конуса, без проведения расчётов. Один из них подробно описан в статье нашего портала «Как сделать абажур своими руками».

stroyday.ru

Как сделать елку из конуса своими руками

Прекрасное дополнение новогоднего праздника – елка, сделанная своими руками. Для этого необходимо сделать картонный конус любым из приведенных выше способов. Главное, чтобы он был прочным и правильной формы. После стоит приступить к ее украшению.

Дальнейшие действия заключаются в следующем:

Конус полностью обклеивается скотчем. Для обмотки можно использовать пищевую пленку.
Выбираются самые толстые (можно разноцветные) нитки и обмакиваются в клее ПВА. Клей можно предварительно разбавить чистой водичкой из расчета 1:1.
Нитки наматываются вокруг конуса.
Изделие оставляется для полной просушки.
Аккуратно через дно вытаскивается бумажный конус с пленкой. Застывшие нитки в форме конуса остаются невредимыми.
Полученная елка может быть украшена по желанию бантиками, ленточными, бусинками, блестками, декоративными фруктами, сделанными самостоятельно елочными игрушками.

Как сделать конус из железа. Расчет развертки усеченного конуса из листового металла

Иногда возникает задачка – сделать защитный зонтик для вытяжной либо печной трубы, вытяжной дефлектор для вентиляции и т.п. Но до этого чем приступить к изготовлению, нужно сделать выкройку (или развертку) для материала. В вебе есть всякие программы для расчета таковых разверток. Но задачка так просто решается, что вы скорее рассчитаете ее с помощью калькулятора (в компьютере), чем будете находить, закачивать и разбираться с этими программами. Начнем с обычного варианта — развертка обычного конуса. Проще всего разъяснить принцип расчета выкройки на примере.

Допустим, нам нужно сделать конус поперечником D см и высотой H см. Совсем понятно, что в качестве заготовки будет выступать круг с вырезанным сектором. Известны два параметра – поперечник и высота. По аксиоме Пифагора рассчитаем поперечник круга заготовки (не путайте с радиусом готового

конуса). Половина поперечника (радиус) и высота образуют прямоугольный треугольник. Поэтому:

Итак, сейчас мы знаем радиус заготовки и можем вырезать круг.

Вычислим угол сектора, который нужно вырезать из круга. Рассуждаем последующим образом: Поперечник заготовки равен 2R, означает, длина окружности равна Пи*2*R — т.е. 6.28*R. Обозначим ее L. Окружность полная, т.е. 360 градусов. А длина окружности готового конуса равна Пи*D. Обозначим ее Lm. Она, естественно, меньше чем длина окружности заготовки. Нам необходимо вырезать сектор с длиной дуги равной разности этих длин. Применим правило соотношения. Ежели 360 градусов дают нам полную окружность заготовки, то разыскиваемый угол должен отдать длину окружности готового конуса.

Из формулы соотношения получаем размер угла X. А вырезаемый сектор находим методом вычитания 360 – Х.

Из круглой заготовки с радиусом R нужно вырезать сектор с углом (360-Х). Не забудьте бросить маленькую полоску материала для нахлеста (если крепление конуса будет внахлест). Опосля соединения сторон вырезанного сектора получим конус данного размера.

Например: Нам нужен конус для зонтика вытяжной трубы высотой (Н) 100 мм и поперечником (D) 250 мм. По формуле Пифагора получаем радиус заготовки – 160 мм. А длина окружности заготовки соответственно 160 x 6,28 = 1005 мм. В тоже время длина окружности подходящего нам конуса — 250 x 3,14 = 785 мм.

Тогда получаем, что соотношение углов будет такое: 785 / 1005 x 360 = 281 градус. Соответственно вырезать нужно сектор 360 – 281 = 79 градусов.

Расчет заготовки выкройки для усеченного конуса

Такая деталь бывает нужна при изготовлении переходников с 1-го поперечника на иной либо для дефлекторов Вольперта-Григоровича либо Ханженкова. Их используют для улучшения тяги в печной трубе либо трубе вентиляции.

Задача мало осложняется тем, что нам неизвестна высота всего конуса, а лишь его усеченной части. Вообщем же начальных цифр здесь три: высота усеченного конуса Н, поперечник нижнего отверстия (основания) D, и поперечник верхнего отверстия Dm (в месте сечения полного конуса). Но мы прибегнем к тем же обычным математическим построениям на базе аксиомы Пифагора и подобия.

В самом деле, разумеется, что величина (D-Dm)/2 (половина разности диаметров) будет относиться с высотой усеченного конуса Н так же, как и радиус основания к высоте всего конуса, как ежели бы он не был усечен. Находим полную высоту (P) из этого соотношения.

Отсюда Р = D x H / (D-Dm).

Теперь зная общую высоту конуса, мы можем свести решение задачки к предшествующей. Рассчитать развертку заготовки как бы для полного конуса, а потом «вычесть» из нее развертку его верхней, ненадобной нам части. А можем рассчитать конкретно радиусы заготовки.

Получим по аксиоме Пифагора больший радиус заготовки — Rz. Это квадратный корень из суммы квадратов высоты P и D/2.

Услуги вальцовки недорого

Компания предоставляет услуги вальцовки по ценам , наиболее приемлемым в Москве. На заказ мы качественно выполним любые объемы работ, в том числе в промышленных масштабах. Изготовим изделия в точности, соответствующие чертежам заказчика. Работы выполняются в оговоренные сроки, без нарушения графиков. Для вальцовки у нас имеется технологически современное оборудование и опытные специалисты, которые относятся к своей работе с максимальной степенью ответственности. Производим вальцевание тонколистового и пруткового металла. Осуществляем вальцовку кромок листа и углов с точным радиусом закругления.