Усеченный конус: формула объема, площади поверхностей и другое

Как построить конус?

Для того, чтобы начать работу, определимся с материалами:

• плотная бумага или бумага для черчения;
• простые карандаши (твердый, средний, мягкий);
• ластик;
• резак.

Лучше всего рисовать на вертикальной плоскости, чтобы избежать искажений.

Этап 1.

Намечаем простым карандашом композицию конуса — его расположение в пространстве листа. Конус не должен утыкаться в края, со всех сторон должно оставаться свободное место.

Рисуя с натуры, придерживайтесь пропорций реального предмета.

Этап 2.

Задайте свободно ширину основания конуса, после чего вложите эту ширину в высоту конуса и проведите перпендикулярную ось по отношению к основанию.

Этап 3

Строим основание — это эллипс, его раскрытие зависит от его расположения относительно линии горизонта. Раскрытие также можно понять с помощью наклона карандаша.

Этап 4

От высоты конуса откладываем прямые, которые касаются эллипса.

Какую фигуру будем изучать?

Круглый прямой усеченный конус представляет собой два круга, имеющих разный диаметр, которые расположены в параллельных плоскостях. Окружности этих кругов соединены прямыми отрезками равной длины, именуемых образующими фигуры. Расстояние между круглыми основаниями называется высотой. Описанная фигура показана ниже на фото.

Получить ее можно двумя принципиально отличающимися геометрическими способами. Во-первых, можно взять обычный круглый конус и параллельной его основанию плоскостью отсечь верхнюю часть. Такое действие приведет к образованию верхнего (малого) основания усеченного конуса. Во-вторых, можно взять трапецию с двумя прямыми углами и вращать ее вокруг стороны, ограниченной этими углами. Сторона трапеции, вокруг которой будет происходить вращение, называется осью фигуры. Две параллельные стороны трапеции опишут круглые основания во время вращения, а четвертая наклонная сторона образует боковую поверхность фигуры.

Схема выше демонстрирует получение усеченного конуса с помощью сечения плоскостью.

Виды вальцевания

К основным видам вальцовки относятся следующие:

• Вальцевание труб (развальцовка) — применяется для изменения радиуса трубы.
• Вальцовка листового металла — процедура сгибания листа металла в радиус.

Вальцовка труб осуществляется на трубогибных станках, которые способны выполнить вальцевание труб диаметром до 30 см. На таком же оборудовании обрабатываются уголки, швеллеры и прочие детали.

Вальцевание в радиус применяется для нержавеющих, черных, оцинкованных металлов различной толщины: стали, алюминия, меди. Для листов с толщиной свыше 10 мм требуется разогрев. Металлические листы до 10 мм толщиной сгибаются в холодном состоянии. Один из более сложных технологических процессов вальцевания листового металла

— это изготовление конусов. Также у нас имеется оборудование, на котором производятся конические и цилиндрические обечайки.

Если вам требуется вальцовка листового металла в Москве

— наша компания готова выполнить услуги под заказ качественно, на высоком профессиональном уровне. Мастера обладают колоссальным опытом и изготавливают детали с максимально точным радиусом. Они досконально знают принцип работы оборудования, скрупулезно соблюдают технологию, придерживаются всех нюансов обработки металла.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Усеченный конус. Усiчений конус

Часть конуса, заключенная между его основанием и некоторой плоскостью, которая параллельная основанию и пересекает конус, называется усеченным конусом.

Частина конуса, укладена між його основою і деякою площиною, яка паралельна основи і перетинає конус називається усіченим конусом.

D1 – верхнее основание; D – нижнее основание. Высотой усеченного конуса называется расстояние между плоскостями оснований. Усеченный конус, который является частью прямого конуса, можно получить вращением прямоугольной трапеции OO1D1D вокруг ее высоты OO1. По аналогии с цилиндром и призмами вводятся понятия описанной около конуса и вписанной в конус пирамиды.

D1 — верхня основа; D — нижня основа. Висотою конуса називається відстань між площинами основ. Усічений конус, який є частиною прямого конуса, можна отримати обертанням прямокутної трапеції OO1D1D навколо її висоти OO1. За аналогією з циліндром і призмами вводяться поняття описаної близько конуса і вписаною в конус піраміди.

Какой инструмент используется для забивания иглы абиссинского колодца?

Кувалда

Самый простой и варварский способ забить иглу – кувалдой. Если у Вас есть опыт аккуратного обращения с этим могучим инструментом, возможно даже всё закончится хорошо и никакое резьбовое соединения у Вас под землей не треснет. Плюсы данного способа – кувалду легко найти, не нужно заморачиваться со специальным оборудованием для забивания. Минусы – при ударах кувалдой невозможно направить всю энергию удара вниз, строго по оси скважинной иглы. А значит, труба будет гнуться набок, плющится. Нагрузка на резьбовые соединения увеличивается. Если Вы приняли решение забивать иглу кувалдой, не бейте по куску трубы, который засаживаете в землю. Накрутите на трубу стальную муфту и используйте кусок трубы с резьбой, ввинтив ее в муфту. Такие наконечники трубы продаются в строительных магазинах под наименованием «резьба» и стоят копейки. Сплющили одну – заменили и продолжили забивать дальше.

Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.

При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

Обратите внимание!

Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.

Хотелось бы рассмотреть ещё несколько понятий по этой теме:

1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:

Важно!

Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.

2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

3. Касательная— это плоскость, которая соприкасается с образующей конуса

При этом важно, чтобы она была перпендикулярна осевому сечению

Как построить развертку поверхности прямого усеченного конуса

Делим основание конуса на 12 равных частей (вписываем правильную пирамиду). Данные элементы построения уже готовы из чертежа «Сечение конуса плоскостью частного положения».

Строим развертку боковой поверхности конуса, которая представляет собой круговой сектор. Центр его радиуса принимается за вершину конуса, а величина радиуса кругового сектора конуса равна длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса. На дугу сектора переносим 12 хорд, которые определят ее длину, а также угол кругового сектора.

К центральной точке дуги сектора боковой развертки усеченного конуса пристраиваем основание конуса. Его основание проецируется в натуральную величину на горизонтальную плоскость проекции.

На развертке конуса к его основанию пристраиваем натуральную величину сечения.

Две крайние образующие конуса, которые формируют его основной контур, проецируются на фронтальную плоскость проекции в натуральную величину, поэтому их можно сразу переносить на развертку боковой поверхности конуса. Так как часть его срезана фронтально проецирующей плоскостью, то перенесем на развертку конуса только крайнюю правую усеченную образующую. Остальные усеченные образующие конуса проецируются на фронтальную плоскость проекций с искажением. Их натуральную величину находят способом вращения вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.

Сам принцип нахождения натуральных величин образующих усеченного конуса сводится к тому, что проводят из точек пересечения образующих с плоскостью горизонтальную прямую до крайней правой (левой) образующей и на ней отмеряют натуральные их величины. Все действия проводят на фронтальной плоскости проекции.

На каждой образующей, лежащей на развертке боковой поверхности конуса, откладываем действительные длины усеченных образующих. Полученные точки соединяем плавной кривой линией команда Сплайн в Автокад.

Мы выполнили задачу начертательной геометрии на построение развертки усеченного конуса, но чтобы не возникло проблем во время ее защиты (когда я обучался, каждая курсовая по начертательной геометрии защищалась), еще раз рассмотрим принцип вращения для нахождения натуральной величины усеченной образующей конуса.

«Их натуральную величину находят способом вращения вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.» Когда мы вращаем образующую прямого конуса до положения параллельного фронтальной плоскости проекции, то ее траектория описывает дугу на горизонтальной плоскости проекции, а на фронтальной прямую!

Вы можете не проводить линии связи с горизонтальной плоскости проекции на фронтальную, ведь очевидно, что точка будет лежать на крайней основной образующей контура конуса для каждой образующей при нахождении ее натуральной величины. Поэтому сам принцип вращения по нахождению натуральной величины образующих конуса сводится к проведению из точек усеченных образующих горизонтальной прямой до основной образующей контура конуса.

В видеоуроке очень наглядно и подробно показан принцип построения развертки прямого усеченного конуса.

Учимся делать усеченный конус или круглый переход своими руками

В быту конечно приходится все делать самому, если есть свое подворье, дом, дача, строительство. Возможно маленький совет в статье с разделами о том, как сделать своими руками конус или переход, поможет вам по хозяйству, без лишних затрат.

Например возьмем ведро сделанное из металла или другого материала. В нем присутствует два различных диаметра. Самый меньше сделан внизу с закрытым дном. Ведро сделано в виде усеченного конуса.

Круглые переходы применяются везде на примере вентиляция, с одного круглого диаметра на другой размером круглый диаметр, тоже в виде усеченного конуса.

Берем случайный размер конуса диаметром 250 х 150 мм высотой 180 мм (у вас свои размеры). Рисунок А.

Делаем выкройку детали по которой создадим переход. Первый диаметр 250 мм умножаем на П=3,14 получается 785 мм. Затем 785 мм делим на 10 частей. Полученную сумму 78,5 мм делим на 2 части. Смотрите пример на рисунке.

Далее рисуем шаблон детали, по ней будем делать выкройку конуса. Рисунок Б.

Шаблон детали обводим 10 раз. У вас получается развертка усеченного конуса. Рисунок В.

Желтым цветом обозначены замки или соединения. Как будете вы соединять ваше право. Замки для плотности, можно на болты, саморезы, сварочный шов, клей, нахлестку. Единственное не забываем добавлять на соединение. Когда полностью обведете шаблон закруглите немного прямые концы.

Далее после сборки конуса, по краям отбортуйте молотком кромку конуса, для закрепления прямой обечайки. Высоту обечайки лучше сделать больше 60 мм.

Первую выкройку лучше сделать пробу из бумажного картона, не испортите материал.

Как сделать конус из железа. Расчет развертки усеченного конуса из листового металла

Иногда возникает задачка – сделать защитный зонтик для вытяжной либо печной трубы, вытяжной дефлектор для вентиляции и т.п. Но до этого чем приступить к изготовлению, нужно сделать выкройку (или развертку) для материала. В вебе есть всякие программы для расчета таковых разверток. Но задачка так просто решается, что вы скорее рассчитаете ее с помощью калькулятора (в компьютере), чем будете находить, закачивать и разбираться с этими программами. Начнем с обычного варианта — развертка обычного конуса. Проще всего разъяснить принцип расчета выкройки на примере.

Допустим, нам нужно сделать конус поперечником D см и высотой H см. Совсем понятно, что в качестве заготовки будет выступать круг с вырезанным сектором. Известны два параметра – поперечник и высота. По аксиоме Пифагора рассчитаем поперечник круга заготовки (не путайте с радиусом готового

конуса). Половина поперечника (радиус) и высота образуют прямоугольный треугольник. Поэтому:

Итак, сейчас мы знаем радиус заготовки и можем вырезать круг.

Вычислим угол сектора, который нужно вырезать из круга. Рассуждаем последующим образом: Поперечник заготовки равен 2R, означает, длина окружности равна Пи*2*R — т.е. 6.28*R. Обозначим ее L. Окружность полная, т.е. 360 градусов. А длина окружности готового конуса равна Пи*D. Обозначим ее Lm. Она, естественно, меньше чем длина окружности заготовки. Нам необходимо вырезать сектор с длиной дуги равной разности этих длин. Применим правило соотношения. Ежели 360 градусов дают нам полную окружность заготовки, то разыскиваемый угол должен отдать длину окружности готового конуса.

Из формулы соотношения получаем размер угла X. А вырезаемый сектор находим методом вычитания 360 – Х.

Из круглой заготовки с радиусом R нужно вырезать сектор с углом (360-Х). Не забудьте бросить маленькую полоску материала для нахлеста (если крепление конуса будет внахлест). Опосля соединения сторон вырезанного сектора получим конус данного размера.

Например: Нам нужен конус для зонтика вытяжной трубы высотой (Н) 100 мм и поперечником (D) 250 мм. По формуле Пифагора получаем радиус заготовки – 160 мм. А длина окружности заготовки соответственно 160 x 6,28 = 1005 мм. В тоже время длина окружности подходящего нам конуса — 250 x 3,14 = 785 мм.

Тогда получаем, что соотношение углов будет такое: 785 / 1005 x 360 = 281 градус. Соответственно вырезать нужно сектор 360 – 281 = 79 градусов.

Расчет заготовки выкройки для усеченного конуса

Такая деталь бывает нужна при изготовлении переходников с 1-го поперечника на иной либо для дефлекторов Вольперта-Григоровича либо Ханженкова. Их используют для улучшения тяги в печной трубе либо трубе вентиляции.

Задача мало осложняется тем, что нам неизвестна высота всего конуса, а лишь его усеченной части. Вообщем же начальных цифр здесь три: высота усеченного конуса Н, поперечник нижнего отверстия (основания) D, и поперечник верхнего отверстия Dm (в месте сечения полного конуса). Но мы прибегнем к тем же обычным математическим построениям на базе аксиомы Пифагора и подобия.

В самом деле, разумеется, что величина (D-Dm)/2 (половина разности диаметров) будет относиться с высотой усеченного конуса Н так же, как и радиус основания к высоте всего конуса, как ежели бы он не был усечен. Находим полную высоту (P) из этого соотношения.

Отсюда Р = D x H / (D-Dm).

Теперь зная общую высоту конуса, мы можем свести решение задачки к предшествующей. Рассчитать развертку заготовки как бы для полного конуса, а потом «вычесть» из нее развертку его верхней, ненадобной нам части. А можем рассчитать конкретно радиусы заготовки.

Получим по аксиоме Пифагора больший радиус заготовки — Rz. Это квадратный корень из суммы квадратов высоты P и D/2.

устройство для проточного хромирования

Так автомобиль содержит для с шестигранным хвостовиком 16 деталей включая двигатель развертка усеченного конуса с эксцентриситетом, крупный карусельный станок имеет более 20 деталей и т.

Чтобы выполнять свои функции в машине детали соединяются между собой определенным образом, образуя подвижные и неподвижные соединения.

❻

Например, соединение коленчатого вала двигателя с шатуном, поршня с гильзой цилиндра подвижные соединения. Соединение штока гидроцилиндра с поршнем, крышки разъемного подшипника с корпусом неподвижное соединение.

Подвижные соединения определяют кинематику машины, а неподвижные — позволяют расчленить машину на отдельные блоки, элементы, детали. С точки зрения общности расчетов все соединения развертка усеченного конуса с эксцентриситетом на две большие группы: неразъемные и https://rudesign24.ru/салфетки-для-чистки-жк-телевизоров соединения.

❻

Неразъемными называют соединения, которые невозможно разобрать без разрушения или повреждения деталей. К ним относятся заклепочные, сварные, клеевые соединения, а также соединения с гарантированным натягом.

Неразъемные соединения осуществляются силами молекулярного сцепления сварка, пайка, склеивание или механическими средствами клепка, вальцевание, прессование. Разъемными называют соединения, которые можно многократно собирать и разбирать без повреждения деталей. К разъемным относятся резьбовые, шпоночные и шлицевые соединения, штифтовые и клиновые соединения.

По форме сопрягаемых поверхностей соединения делят на плоское, цилиндрическое, коническое, сферическое, винтовое и т. Проектирование соединений является очень ответственной задачей, поскольку https://rudesign24.ru/телевизор-тухнет-экран-через-некоторое-время разрушений в машинах происходит именно в местах соединений.

Развертка усеченного конуса

К соединениям в зависимости от их назначения предъявляются требования прочности, плотности герметичности и жесткости. При оценке прочности соединения стремятся приблизить его прочность к прочности соединяемых элементов, то есть стремятся обеспечить равнопрочность конструкции.

❻

Требование плотности является основным для сосудов и аппаратов, работающих под давлением. Уплотнение разъемного соединения достигается за счет: 1 сильного сжатия достаточно качественно обработанных поверхностей; 2 введения прокладок из легко деформируемого материала.

❻

Выбор типа соединения определяет инженер. Терминология Простейшая классификация крепёжных изделий может проводиться по нескольким направлениям: резьбовые и без резьбы, стержневые и с функциональным отверстием, изделия типа болт с невыпадающей шайбой относят к комбинированным и т.

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Круглый конус в геометрии

Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.

Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.

Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.

Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.

Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.

Обозначение конусности на чертеже

При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем

Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:

1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
2. Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
3. Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
4. На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.

Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:

1. Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
2. В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
3. При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
4. Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.

На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.

Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:

1

Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2

Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3

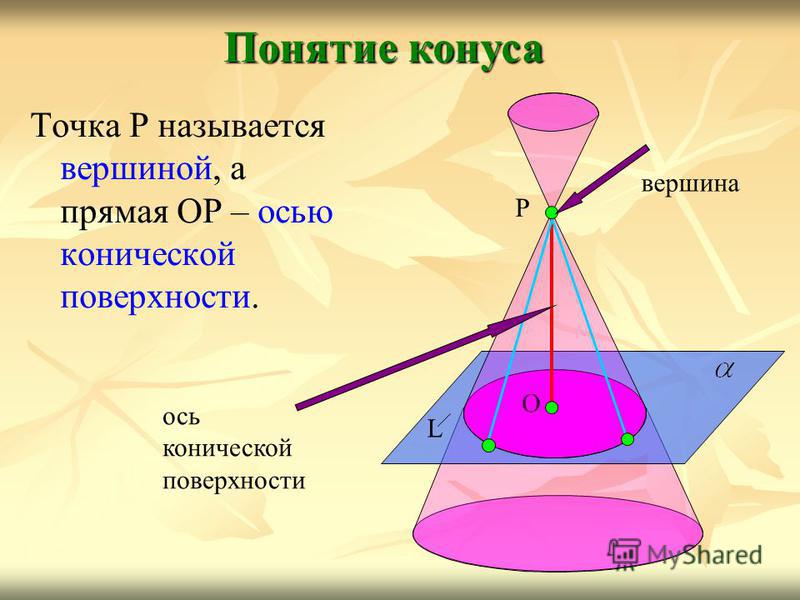
Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности

4

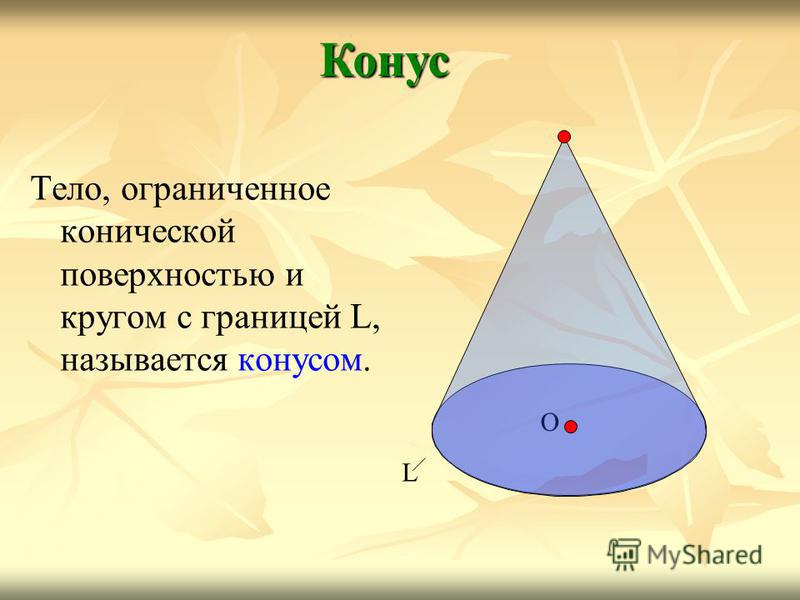
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L

5

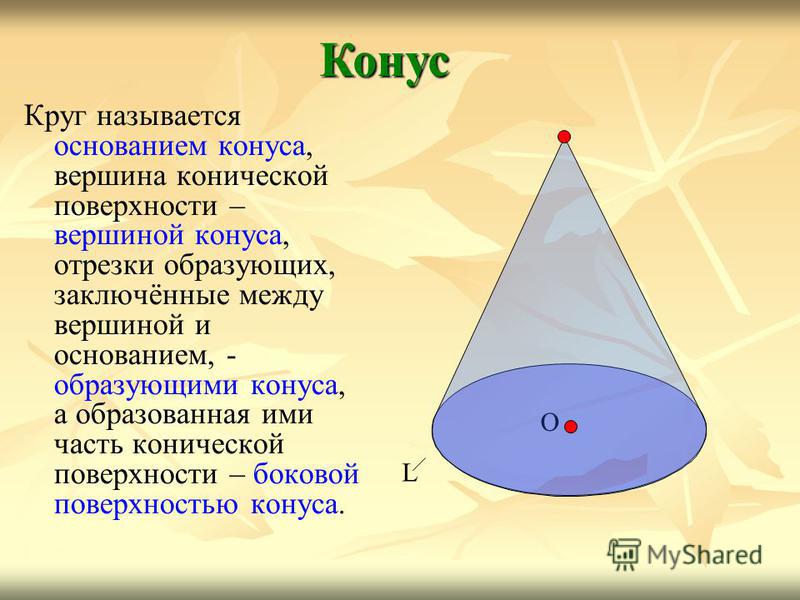
Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L

6

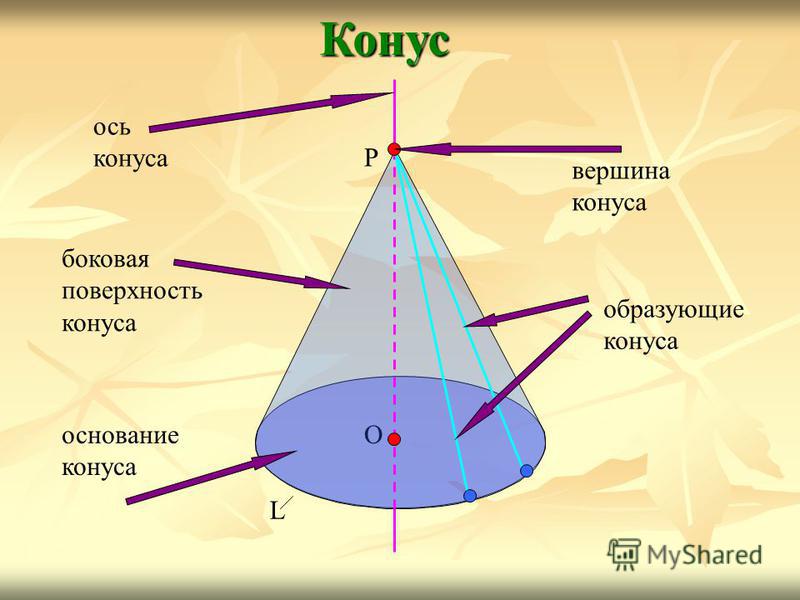
Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса

7

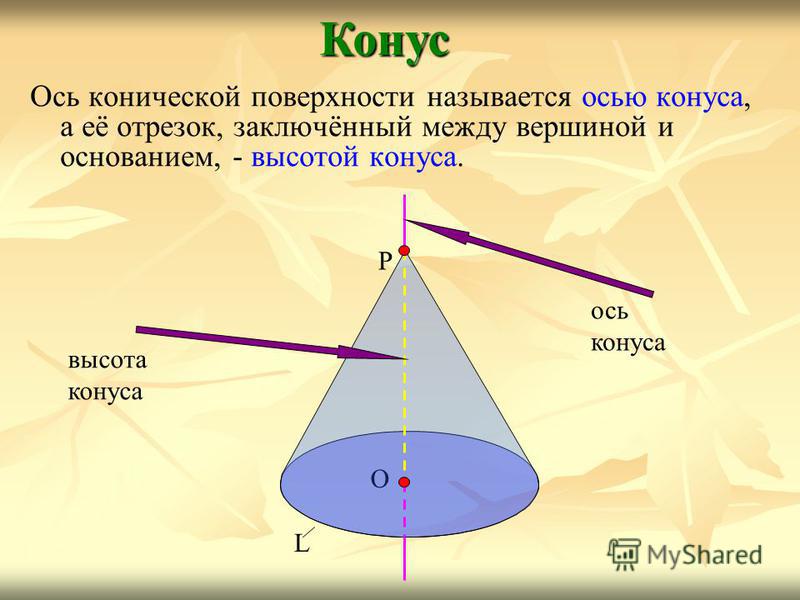
Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса

8

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10

Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1

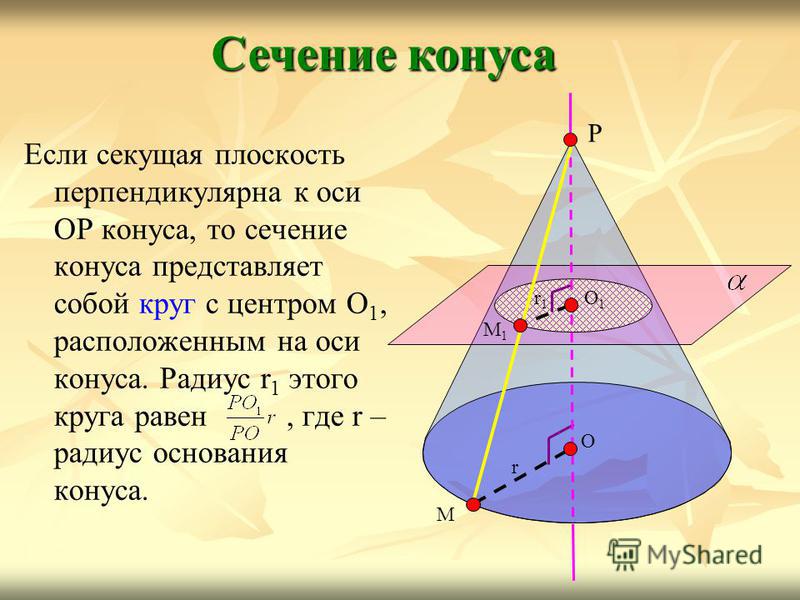
11

Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12

За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r

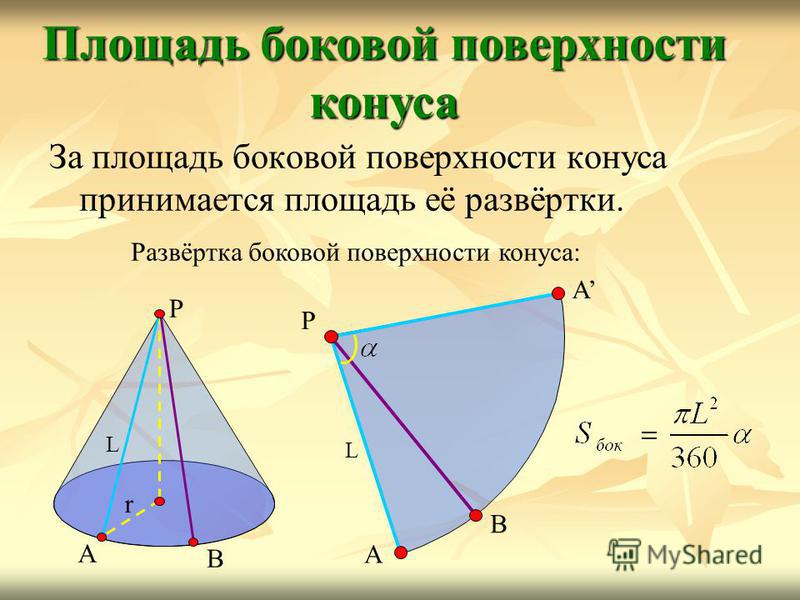
13

Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15

Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус

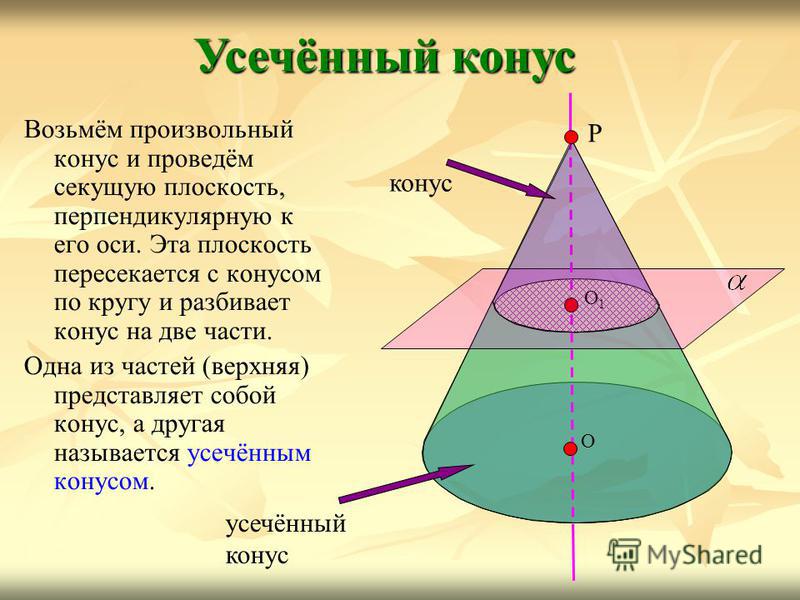
16

Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота

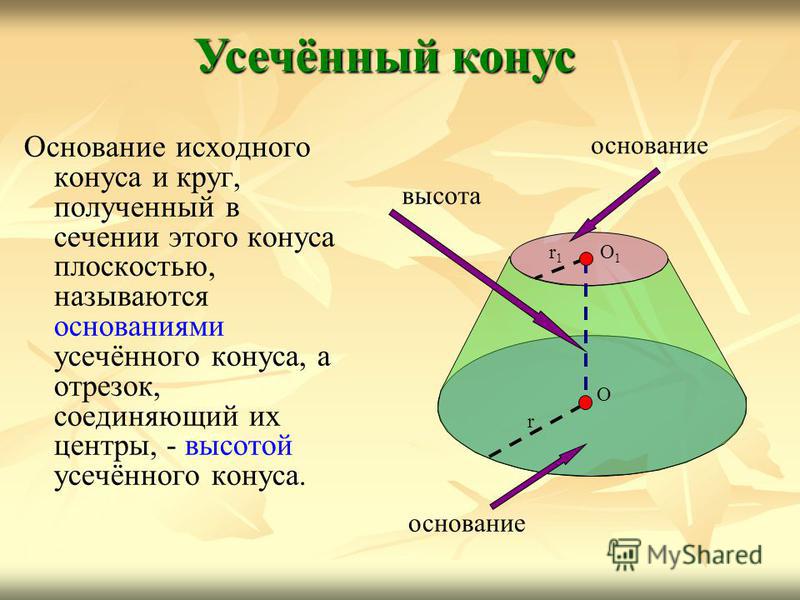
17

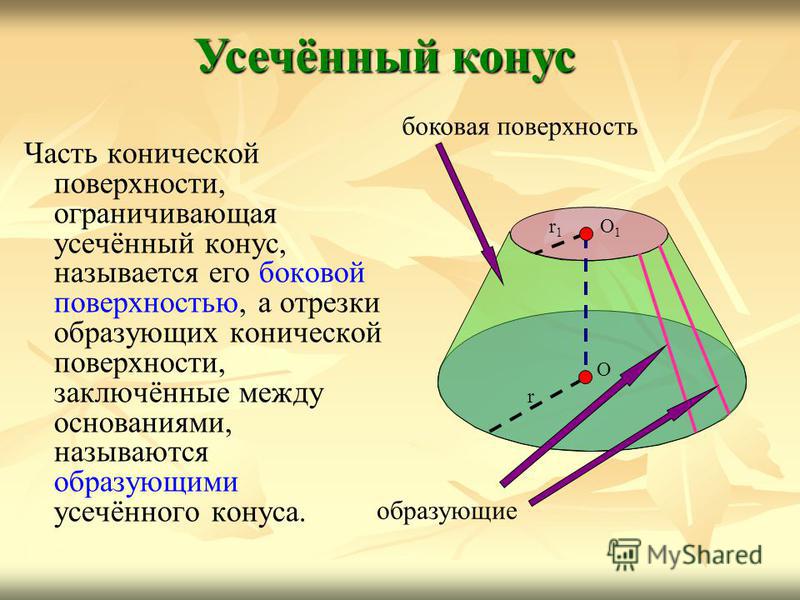
Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие

18

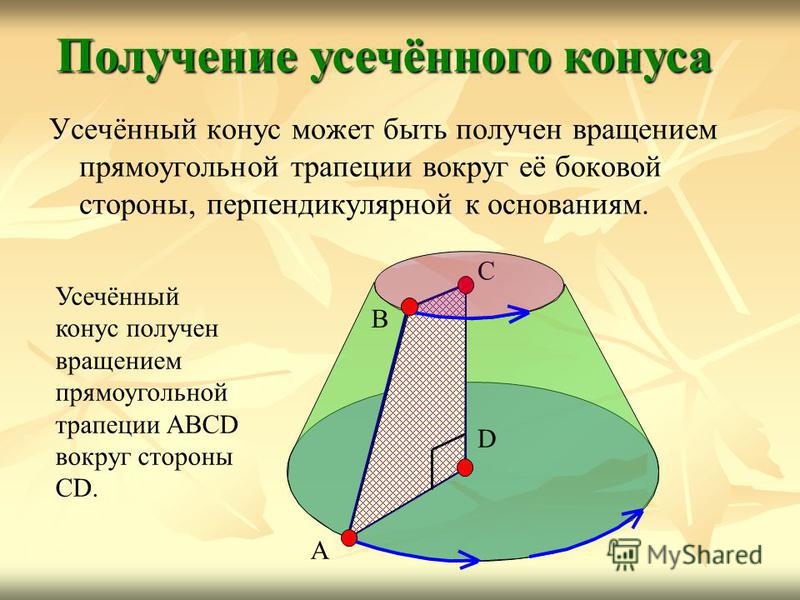
Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.

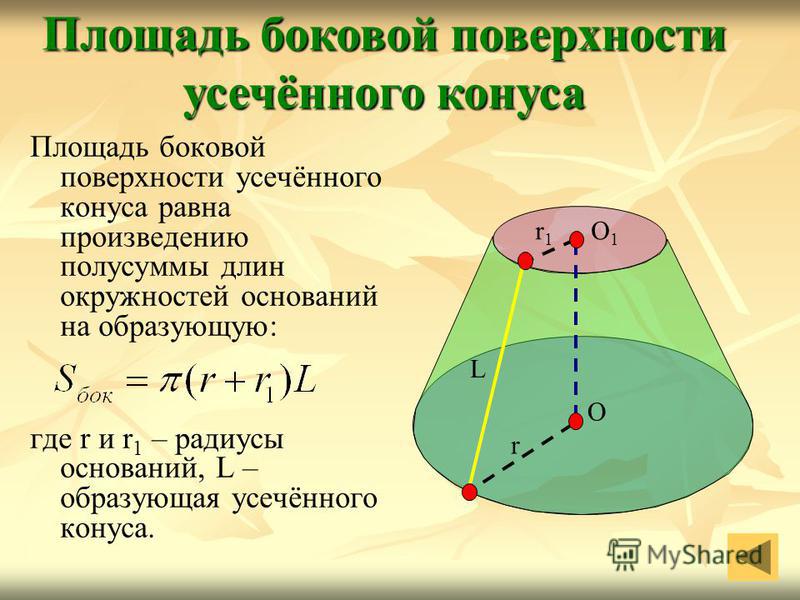
19

Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L