Как найти образующую конуса обычного и усеченного. формулы
Содержание:
- Как сделать конус из картона
- Обозначение на чертежах
- Площадь боковой поверхности конуса через его радиус и высоту
- Объем пирамиды
- Несоответствия между американской и российской метрической системами
- Специфика развертывания конусов
- О какой фигуре будет идти речь?
- Системы обозначения конусов Морзе
- Площадь боковой поверхности конуса через его радиус и направляющую
- История создания
- Особенности конструкции и основные типы конусов Морзе
- История создания
- Площадь боковой поверхности конуса через его радиус и направляющую
- История создания
- Вычисление диаметра через площадь поверхности и генератрису
- Объем
- Угол конуса
- Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:
- Генератриса усеченной фигуры
- Определение диаметра через объем и высоту
Как сделать конус из картона
Вы узнали, как сделать конус из простой бумаги А4, но, если вам нужна плотная поделка, лучше воспользоваться картоном. Материалы и инструменты остаются теми же, что и в предыдущих поделках. Различие заключается только в оттенке картона, его подбираем исходя из предназначения.
Будущий конус будет достаточно прочным за счет чего, его применение может быть широким. Подобную методику работы мы уже рассмотрели выше, но это изготовление все же отличается.
Начнем:
- Возьмите картон нужного оттенка. Определите середину листа и используя циркуль начертите круг.
- Полученную окружность нужно разделить на четыре равные доли. Для разделения фигуры на правильные части проведите через полученную ранее точку в центре прямые линии.
- Складываем круг в разных направлениях. Вы получите четыре сегмента. Один из них нужно вырезать.
- Полученную заготовку сворачиваем образуя колпак. Так как картон может не сразу склеиться, закрепляем низ фигуры степлером. И только затем промазываем фигуру ПВА.
Плотный конус готов. Если вам нужна не одна геометрическая фигура, а несколько, первый полученный круг, в котором уже вырезана одна четверть, можно использовать в качестве шаблона.
Обозначение на чертежах
Обозначение трубной конической резьбы:
- R — внешняя коническая;
- RC — конические пазы внутреннего типа;
- RP — внутренняя коническая с цилиндрическим профилем;
- LH — левая;
- RH — правая;
- MK — конусная метрическая;
- M — метрическая;
- K — дюймовая коническая;
- укор. — укороченный профиль;
- пов. точ. — повышенная точность нарезки.
На чертеже обозначение выносят при помощи выноски на полке, стрелка указывает на основную линию. Длины нарезки не указываются, поскольку является стандартной. Коническая резьба указывается в виде дробной величины: числителем выступает маркировка внутренней нарезки, а знаменателем — наружной.
Основная плоскость резьбы обозначается сплошной тонкой линией.
Площадь боковой поверхности конуса через его радиус и высоту
Очень часто в задачах на вычисление площади боковой поверхности конуса известна высота конуса вместо его направляющей.Так как конус прямой, то треугольник AOS – прямоугольный, где AO и OS – катеты, а AS –гипотенуза. Воспользовавшись теоремой Пифагора, получаем: Отсюда: Но Тогда:Подставим данное выражение в формулу площади боковой поверхности конуса: Боковая поверхность конуса равна произведению числа на радиус конуса и корень квадратный из суммы квадратов радиуса и высоты конуса
Пример расчета площади боковой поверхности конуса, если известны его радиус и высота.Найти площадь боковой поверхности конуса с радиусом равным 1 см и высотой, равной 5 смПо условию задачи Н = 5см, R=1смФормула боковой поверхности конуса:Подставив в формулу значения из условия задачи, имеем:
Объем пирамиды
Для начала рассмотрим треугольную пирамиду. Вершину пирамиды примем за начало координат точку О, а ось Ох проведем перпендикулярно основанию, причем ось будет направлена от вершины пирамиды к основанию.
Пусть ось Ох пересечет основание АВС в точке М. Тогда ОМ – это высота, чью длину мы обозначим как h.
Далее построим сечение А1В1С1, параллельное АВС. Это сечение пересечется с ОМ в точке ОМ1. Тогда ОМ1 – это координата х, характеризующая расположение сечения А1В1С1.
Осталось составить выражение для площади ∆А1В1С1. Так как АВ||A1B1, то ∠АВО и ∠А1В1О одинаковы как соответственные углы. Тогда у ∆АВО и ∆А1В1О есть два равных угла (ведь ∠АОВ у них общий), а потому эти треугольники подобны по первому признаку подобия. Это означает, что
Надо как-то найти значение коэффициента k, который, очевидно, как-то зависит от переменной х. Рассмотрим теперь ∆ОМВ и ∆ОМ1В1. Они прямоугольные, ведь ОМ перпендикулярен плоскостям этих треугольников. Также у них есть общий угол ∠ОВМ. Значит, они подобны, и поэтому
Итак, если пирамида имеет высоту h и площадь основания S, то объем пирамиды равен:
Выведенная нами формула справедлива для треугольной пирамиды. Однако если в основании пирамиды лежит произвольный многоугольник, то, разбив этот многоугольник на треугольники, мы разобьем и пирамиду на несколько треугольных пирамид. У них будет общая высота h и площади оснований S1, S2, S3…, которые в сумме составляют площадь многоугольника S.
Объем треугольных пирамид рассчитывается по выведенной нами формуле:
Задание. В основании пирамиды высотой 15 лежит квадрат со стороной 4. Вычислите ее объем.
Решение. Сначала находим площадь основания. Для этого надо сторону квадрата умножить саму на себя:
Задание. В кубе АВСDA1В1С1D1 отмечены точки Е и F – середины ребер ВС и CD соответственно. Во сколько раз объем пирамиды С1EFC меньше объема куба?
Решение. Обозначим длину ребра куба буквой а. Тогда его объем рассчитывается так:
Задание. Отрезок MN перпендикулярен плоскости пятиугольника АВСDE. Точка K, принадлежащая этой плоскости, делит отрезок MN в отношении 2:1. Во сколько раз объем пирамиды MABCDE больше объема пирамиды NABCDE?
Решение. Запишем формулы для объемов этих пирамид. При этом учтем, что MK – высота для MABCDE, а NK – это высота для NABCDE.
Далее рассмотрим такую фигуру, как усеченная пирамида. Ясно, что ее объем можно вычислить, если из объема исходной пирамиды вычесть объем отсеченной верхушки.
Снова рассмотрим пирамиду ОАВС, через которую проведено сечение А1В1С1, параллельное основанию.
Обозначим площадь нижнего основания пирамиды как S2, а площадь верхнего основания – как S1. Далее высоту усеченной пирамиды (отрезок ММ1) обозначим как h. Мы уже выяснили ранее, что основания АВС и А1В1С1 – это подобные треугольники, причем коэффициент их подобия k равен отношению высот ОМ и ОМ1. Тогда можно записать:
Далее используем основное свойство пропорции:
Далее числитель дроби мы раскладываем на множители, используя формулу разности кубов:
Задание. Основаниями усеченной пирамиды являются квадраты со сторонами 9 см и 5 см, а высота пирамиды составляет 6 см. Найдите ее объем.
Сначала вычислим площади оснований:
Несоответствия между американской и российской метрической системами
В настоящее время пролювий с американской гравировкой КМ7 не соответствует российским стандартам. В России долгое время используют метрический штекель с конусом №80. Иногда оказывается, что использовать американский конус использовать неудобно – его длина не соответствует стандартам станка.
По этой причине пришлось удалить его толстую часть, и в настоящее время имеется девять размеров с более укороченным креплением. Хвостовая часть конуса Морзе за №80 может изготавливаться с различными вариациями. Но принцип их использования остается на высоком уровне и не требует особой спецподготовки.
КМ – это горнитос Морзе, который спроектирован компанией Кеннаметал. И в настоящее время является одним из наиболее часто используемых креплений инструмента. Такое положение дел является следствием длительного периода использования именно данного пролювия, ибо диапазон размеров в высшей степени зависит от того, насколько эффективно используется инструмент.
Очевидно одно: конус Морзе является сегодня наиболее часто используемым креплением для самых разных составляющих.
Специфика развертывания конусов
Отверстия конической формы, отличающиеся нормализованными размерами необходимо обрабатывать развертками. Набор этих инструментов представлен на рисунке 1. В него входят три предмета конкретного типа и геометрических параметров, соответствующих обрабатываемому отверстию.
Рисунок 1. Развертки конической формы: а – для обдирочных работ; б – для измельчения снимаемой стружки; в – для чистовых работ
У каждой развертки, изображенной на рисунке 1, присутствует коническая режущая часть, размеры которой выбираются по отверстию, и хвостовик в форме цилиндра. Конструкционное исполнение конической части предусматривает наличие специальных канавок, образующих зубья.
Обдирочная развертка (рисунок 1,а) располагает небольшим количеством зубьев. Все они располагаются ступенчато по винтовой линии. Инструмент, представленный на рисунке 1, б имеет гораздо больше зубьев, которые так же, как и в первом варианте, размещены ступенчато. Характерной особенностью чистовой развертки (рисунок 1, в) являются прямые зубья.
Перед использованием разверток необходимо позаботиться о сверлении отверстия. Для этого выбирается сверло, диаметр которого где-то на полмиллиметра меньше диаметра обдирочной развертки. После сверления отверстия можно приступать к его развертыванию, в результате которого обрабатываемая поверхность становится не только конической, но и ступенчатой. Обработка вторым инструментом из набора способствует уменьшению ступеней и увеличению их количества. При использовании третьей развертки имеющиеся ступени сглаживаются.
Комплект, используемый для обработки отверстий с небольшим уклоном конуса, может состоять всего лишь из пары инструментов. Пологие конусы допускается обрабатывать чистовой разверткой.
Проверять параметры полученных отверстий проще всего калибр-пробкой, изображенной на рисунке 2.
Рисунок 2. Проверочная калибр-пробка: а — внешний вид; б — схема применения инструмента; А и В — риски, обозначающие предельные допуски угла конуса
Используя представленный выше калибр, на его боковой поверхности можно делать специальные отметки при помощи мела/карандаша. При вводе данного приспособления в отверстие его нужно несколько раз провернуть. Полностью стертые отметки будут свидетельствовать о том, что угол конуса отверстия выполнен верно. В случае, когда отметки стираются лишь у меньшего диаметра калибр-пробки, угол конуса выполнен больше, чем нужно. Соответственно, о слишком маленьком угле конуса можно судить по линиям, стертым только у большого диаметра контрольного инструмента.
На рисунке 2, б представлена проверка правильно обработанного конуса, поскольку риска В перекрывается деталью, а риска А — нет. Если бы торец изделия не перекрыл риску В, то отверстие можно обработать еще раз. Если же торец изделия перекрывает риску А, то деталь считается браком. Вместо рисок на инструменте могут предусматриваться специальные уступы, соответствующие проходному/непроходному размеру.
Перейти к списку статей >>
О какой фигуре будет идти речь?
Круглый конус – это фигура, которую можно получить следующим образом. Необходимо взять треугольник с углом прямым и его вокруг одного из катетов вращать. Тогда получится показанная ниже объемная фигура.
Отрезок AC на рисунке называется радиусом основания, который “рисует” при вращении с центром в точке A круг. Катет AB – это высота конуса. Очевидно, что отрезок AB перпендикулярен основанию и является частью оси вращения фигуры. Точка B – это высота рассматриваемой фигуры. Отрезок BE называется образующей, или генератрисой конуса. Совокупность всех генератрис образует боковую поверхность конуса. Она является конической. Ограничивающая основание окружность называется направляющей, или директрисой конуса.
Поскольку генератриса, радиус и высота являются гипотенузой и катетами рассмотренного прямоугольного треугольника, то для них можно записать формулу:
g2 = r2 + h2
Здесь g – генератриса, r – радиус, h – высота.
Системы обозначения конусов Морзе
В России и странах ближнего зарубежья до сих пор принято классифицировать все виды конусов Морзе согласно советским ГОСТам. В них указаны основные параметры (конусность, длина, диаметры наружного и внутреннего конусов) для каждого вида конусов Морзе.
Даже сейчас, когда во всем мире производство инструмента регламентируется международными стандартами ISO и DIN, обозначения ГОСТ обозначения в нашей стране не потеряли свою актуальность. Более того, старые ГОСТы постоянно дорабатываются и совершенствуются.
На данный момент основным документом, регламентирующим обозначения и размеры конусов Морзе является ГОСТ 25557-2006 «Конусы инструментальные. Основные размеры», заменивший устаревший ГОСТ 25557-82. Ниже приведены примеры обозначения конусов Морзе из данного ГОСТ.
Так же существуют госты на отдельные виды инструмента, в которых применена эта конструктивная особенность. Например, ниже приведена таблица обозначений оправок с конусом Морзе для сверлильных патронов (ГОСТ 2682-86).
В соответствие с современными международными стандартами конусы Морзе подразделяются на 8 видов, обозначаемых маркировкой МТ и цифрами от 0 до 7 (например: МТ3), в Германии принята маркировка МК
Площадь боковой поверхности конуса через его радиус и направляющую
Пусть дан конус с радиусом R
и образующей L
AS=L, AO=R
Разрежем конус по образующей L
и развернем его боковую поверхность.
В результате получим криволинейный треугольник ASA`
, где AS=L, A`S=L.
Дуга AA`
-это вытянутая окружность основания конуса с радиусом R
. Следовательно, длина дуги AA`
будет равна 2πR
Площадь боковой поверхности будет равна площади сектора круга с радиусом R
.
Если угол α — радиальная мера угла, то:
где α=∠{ASA`}
Чтобы найти угол ∠{ASA`} воспользуемся формулой длины дуги, которая стягивает данный угол:
Но с другой стороны:
Приравняем правые части равенств. Имеем:
Выразим α:
Подставим полученное выражение в формулу площади сектора:
Следовательно, боковая поверхность конуса равна произведению числа π на радиус конуса и его образующую.
Формула боковой поверхности конуса будет иметь следующий вид:
Наклонные призмы, цилиндры и конусы. Мы видели, что объем правой прямоугольной призмы — это площадь основания, умноженная на высоту. Что произойдет, если основание призмы не находится непосредственно под вершиной? Первый принцип Кавальери гласит, что если сечения двух твердых тел, взятые на том же расстоянии над основанием, имеют одинаковую площадь, то твердые тела имеют одинаковый объем.
Мы не будем приводить доказательства принципа Кавальери здесь. Чтобы представить строгое доказательство, нужны идеи интеграции и резки. Это позволяет нам сказать, что объем любой прямоугольной призмы, прямой или наклонной, определяется площадью основания, умноженной на высоту.
Пример расчета площади боковой поверхности конуса, если известны его радиус и направляющая
Найти площадь боковой поверхности конуса с радиусом равным 3 см, образованным направляющей равной 7 см
По условию задачи L
= 5см, R
=3см
Формула боковой поверхности конуса:
Подставив в формулу значения из условия задачи, имеем:
То же самое относится к наклонным цилиндрам и конусам. Найдите объем цилиндра, показанный на диаграмме. Мы выведем формулу площади поверхности из формулы объема. Самый простой и естественный современный вывод для формулы объема сферы использует исчисление и будет выполнен по старшей математике. Вывод с использованием умного применения принципа Кавальери обсуждается в разделе этого модуля.
Объем радиуса сферы задается формулой. Найдите радиус сферы, верный с точностью до ближайшего миллиметра. Радиус составляет около 87 мм. Исчисление необходимо для получения формулы для площади поверхности сферы строго. Вот интересная формула, которая использует идею аппроксимации сферы пирамидами с общей вершиной в центре сферы.
История создания
Появления такой конструкции, а так же происхождение самого названия до сих пор покрыто множеством тайн. Достоверно известно, что в 1863 году американский инженер Стивен Морзе зарегистрировал патент на изобретение спирального сверла, такого, которое известно нам и по сей день. До этого для изготовления сверла, скручивали заостренный плоский профиль.
В описании, запатентованного Стивеном Морзе спирально м сверле, нет никаких упоминаний об особой форме хвостовика, но по какой-то причине Бюро стандартов США внесло коническую форму в национальные стандарты. Считается, что изобретатель, запатентовав новую конструкцию сверла, направил опытные образцы в Бюро патентов, где была замечена и по достоинству оценена эта особенность.
Впоследствии была создана компания по производству, получившая его имя и занимавшаяся изготовлением инструмента для машиностроения. К концу 19 века компания серьезно расширилась и стала одним из ведущих производителей инструмента того времени. Произведенный ей продукт поставлялся во многие страны мира, в том числе и в Россию. За время ее существования было запатентовано еще несколько изобретений, но, ни одно из них не было связано с коническим исполнением хвостовиков инструмента. Так же есть сведения, что через какое-то время после основания сам изобретатель по неизвестным причинам покинул компанию, при этом его имя в названии сохранилось.
Так же известно еще несколько изобретателей с фамилией Морзе, живших в США в то время. И, возможно, автором этого изобретения является кто-то из них, но никакой информации, подтверждающей эту версию, нет. Поэтому официальным изобретателем конической формы хвостовика инструмента считается именно Стивен Эмброуз Морзе.
Это интересно: Что такое канифоль и для чего она нужна — разбираем досконально
Особенности конструкции и основные типы конусов Морзе
Есть версия, что коническая конструкция появилась в результате постепенной эволюции токарного, фрезерного и сверлильного инструмента в результате изучения влияния износа инструмента на его характеристики и качество выпускаемых деталей. Было замечено, что в процессе работы инструмент с цилиндрическим хвостовиком изнашивался и начинал проворачиваться в кулачках, возникали биения и отклонения инструмента.
В процессе развития технологий машиностроения появился так называемый метрический конус, который отличается от своих предшественников постоянной конусностью и угловыми размерами. Его конусность составляет 1:20, уклон – 1°51’56”, а угол – 1°51’51”, тогда как до этого конусность была переменной и варьировалась от 1:19,002 до 1:20,047.
Согласно классификации, принятой в ГОСТах СССР конусы Морзе принято разделять на малые, большие и общего применения.
Исходя из особенностей конструкции, на сегодняшний день различают три типа конусов Морзе:
- Гладкий;
- С резьбой;
- С лапкой.
Выпадение инструмента из шпинделя предотвращается самой конической формой хвостовика и отверстия в шпинделе или оправке. Дополнительно крепление хвостовика с лапкой в шпинделе происходит за счет вхождения лапки в специальный паз, резьбового – за счет резьбы в торце хвостовика.
Так же изготавливают инструмент с дополнительными пазами и отверстиями для подведения СОЖ. Это наиболее актуально для современных станков с ЧПУ.
История создания
Появления такой конструкции, а так же происхождение самого названия до сих пор покрыто множеством тайн. Достоверно известно, что в 1863 году американский инженер Стивен Морзе зарегистрировал патент на изобретение спирального сверла, такого, которое известно нам и по сей день. До этого для изготовления сверла, скручивали заостренный плоский профиль.
В описании, запатентованного Стивеном Морзе спирально м сверле, нет никаких упоминаний об особой форме хвостовика, но по какой-то причине Бюро стандартов США внесло коническую форму в национальные стандарты. Считается, что изобретатель, запатентовав новую конструкцию сверла, направил опытные образцы в Бюро патентов, где была замечена и по достоинству оценена эта особенность.
Впоследствии была создана компания по производству, получившая его имя и занимавшаяся изготовлением инструмента для машиностроения. К концу 19 века компания серьезно расширилась и стала одним из ведущих производителей инструмента того времени. Произведенный ей продукт поставлялся во многие страны мира, в том числе и в Россию. За время ее существования было запатентовано еще несколько изобретений, но, ни одно из них не было связано с коническим исполнением хвостовиков инструмента. Так же есть сведения, что через какое-то время после основания сам изобретатель по неизвестным причинам покинул компанию, при этом его имя в названии сохранилось.
Так же известно еще несколько изобретателей с фамилией Морзе, живших в США в то время. И, возможно, автором этого изобретения является кто-то из них, но никакой информации, подтверждающей эту версию, нет. Поэтому официальным изобретателем конической формы хвостовика инструмента считается именно Стивен Эмброуз Морзе.
Площадь боковой поверхности конуса через его радиус и направляющую
Пусть дан конус с радиусом R и образующей LAS=L, AO=RРазрежем конус по образующей L и развернем его боковую поверхность.В результате получим криволинейный треугольник ASA` , где AS=L, A`S=L.Дуга AA` -это вытянутая окружность основания конуса с радиусом R. Следовательно, длина дуги AA` будет равна 2πRПлощадь боковой поверхности будет равна площади сектора круга с радиусом R.Если угол α – радиальная мера угла, то: где α=∠{ASA`}Чтобы найти угол ∠{ASA`} воспользуемся формулой длины дуги, которая стягивает данный угол: Но с другой стороны: Приравняем правые части равенств. Имеем: Выразим α: Подставим полученное выражение в формулу площади сектора: Следовательно, боковая поверхность конуса равна произведению числа π на радиус конуса и его образующую.Формула боковой поверхности конуса будет иметь следующий вид:
Пример расчета площади боковой поверхности конуса, если известны его радиус и направляющаяНайти площадь боковой поверхности конуса с радиусом равным 3 см, образованным направляющей равной 7 смПо условию задачи L = 5см, R=3смФормула боковой поверхности конуса:Подставив в формулу значения из условия задачи, имеем:
История создания
Появления такой конструкции, а так же происхождение самого названия до сих пор покрыто множеством тайн. Достоверно известно, что в 1863 году американский инженер Стивен Морзе зарегистрировал патент на изобретение спирального сверла, такого, которое известно нам и по сей день. До этого для изготовления сверла, скручивали заостренный плоский профиль.
В описании, запатентованного Стивеном Морзе спирально м сверле, нет никаких упоминаний об особой форме хвостовика, но по какой-то причине Бюро стандартов США внесло коническую форму в национальные стандарты. Считается, что изобретатель, запатентовав новую конструкцию сверла, направил опытные образцы в Бюро патентов, где была замечена и по достоинству оценена эта особенность.
Впоследствии была создана компания по производству, получившая его имя и занимавшаяся изготовлением инструмента для машиностроения. К концу 19 века компания серьезно расширилась и стала одним из ведущих производителей инструмента того времени. Произведенный ей продукт поставлялся во многие страны мира, в том числе и в Россию. За время ее существования было запатентовано еще несколько изобретений, но, ни одно из них не было связано с коническим исполнением хвостовиков инструмента. Так же есть сведения, что через какое-то время после основания сам изобретатель по неизвестным причинам покинул компанию, при этом его имя в названии сохранилось.
Так же известно еще несколько изобретателей с фамилией Морзе, живших в США в то время. И, возможно, автором этого изобретения является кто-то из них, но никакой информации, подтверждающей эту версию, нет. Поэтому официальным изобретателем конической формы хвостовика инструмента считается именно Стивен Эмброуз Морзе.
Вычисление диаметра через площадь поверхности и генератрису
Поверхность рассматриваемого конуса образована конической поверхностью и круглым основанием. Развертка конуса показана ниже.
Общая площадь развертки определяется по следующей формуле:
Если известна площадь S и генератриса g, тогда это уравнение позволяет вычислить радиус фигуры, а значит, и ее диаметр. Заметим, что речь идет об уравнении второго порядка относительно радиуса r. Решать его следует с использованием дискриминанта. При решении, как правило, получаются два корня, один из которых отрицательный. Он должен быть отброшен, ввиду его не физического значения.
С использованием описанной методики в конце статьи будет решена задача, и будет получен ответ на вопрос о том, чему равен диаметр конуса.
Объем
Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м3. Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.
Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.
Угол конуса
Важным показателем при построении различных чертежей считается угол конуса. Он определяется соотношение большого диаметра к меньшему. Высчитывается этот показатель по следующим причинам:
- На момент обработки мастер должен учитывать этот показатель, так как он позволяет получить требуемое изделие с высокой точностью размеров. В большинстве случаев обработка проводится именно при учете угла, а не показателей большого и малого диаметра.
- Угол конуса рассчитывается на момент разработки проекта. Этот показатель наносится на чертеж или отображается в специальной таблице, которая содержит всю необходимую информацию. Оператор станка или мастер не проводит расчеты на месте производства, вся информация должна быть указана в разработанной технологической карте.
- Проверка качества изделия зачастую проводится по малому и большему основанию, но также могут применяться инструменты, по которым определяется показатель конусности.
Как ранее было отмечено, в машиностроительной области показатель стандартизирован. В другой области значение может существенно отличаться от установленных стандартов. Некоторые изделия характеризуются ступенчатым расположение поверхностей. В этом случае провести расчеты достаточно сложно, так как есть промежуточный диаметр.
Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:
1
Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2
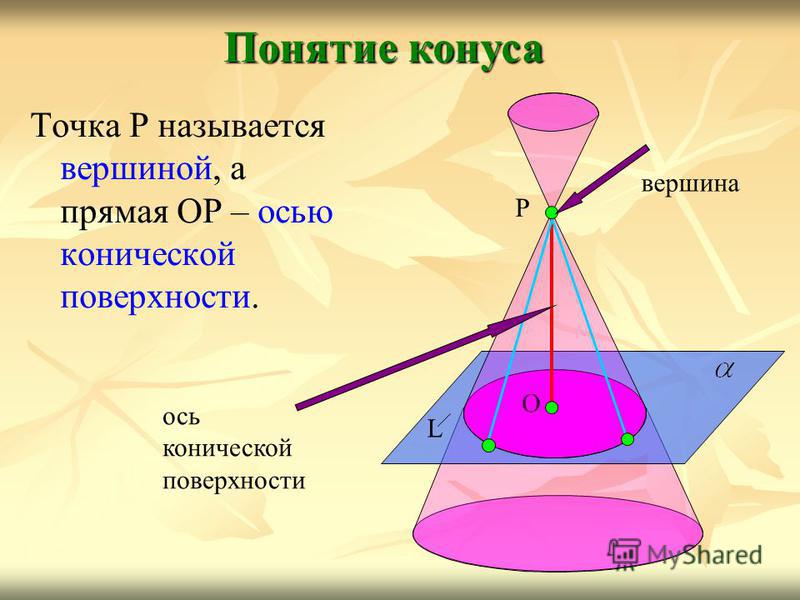
Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3
Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности
4
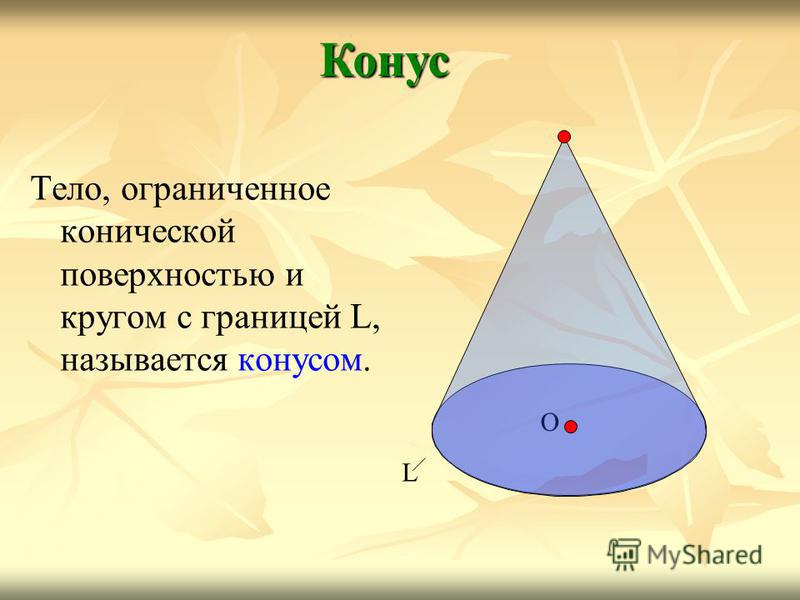
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L
5
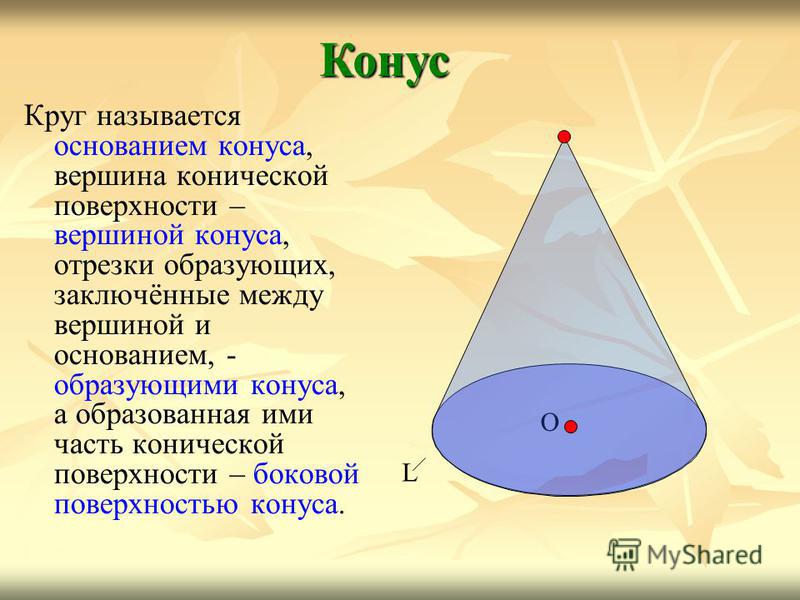
Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L
6
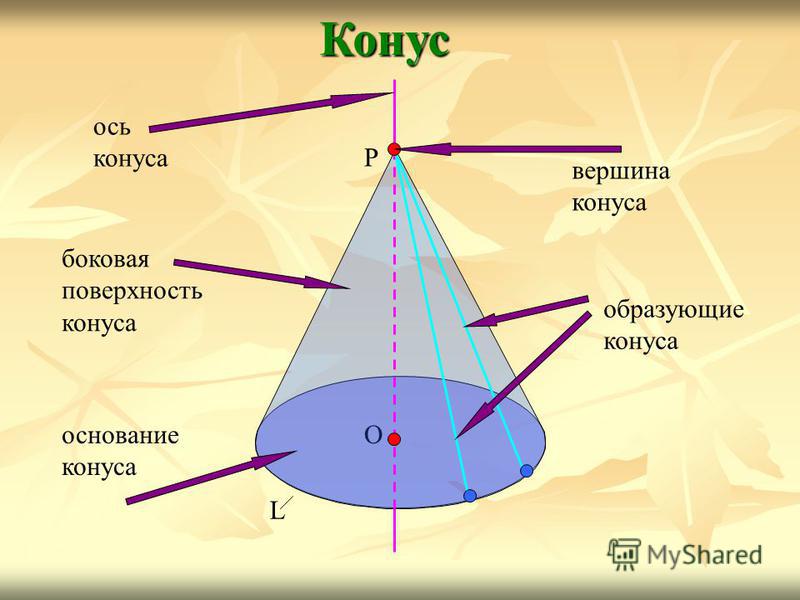
Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса
7
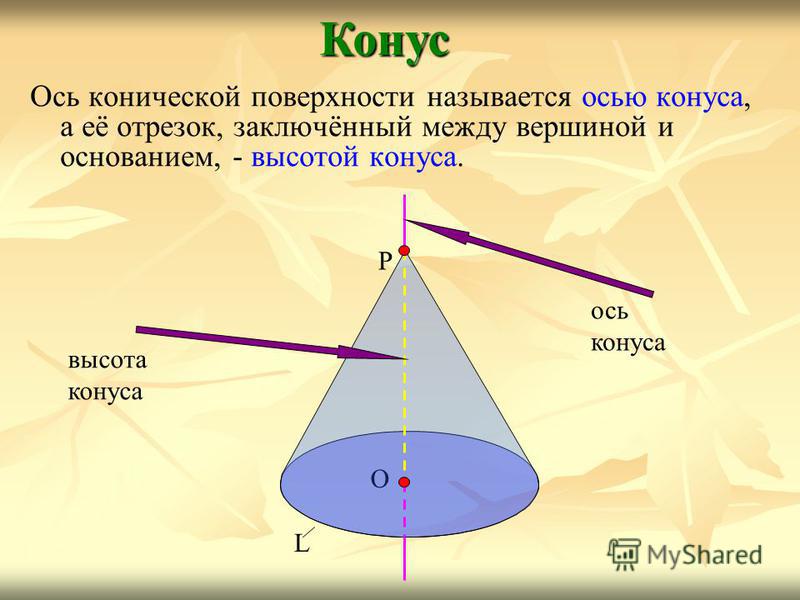
Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса
8
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9
Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10
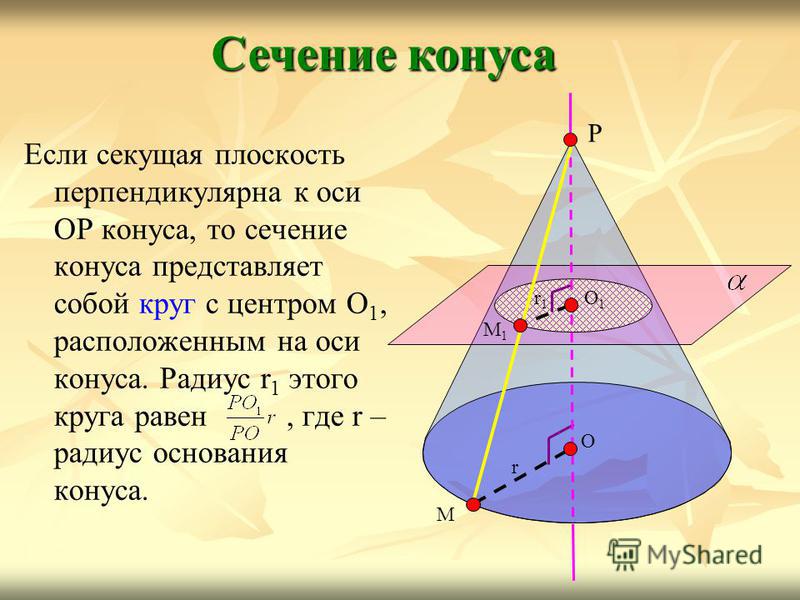
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1
11
Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12
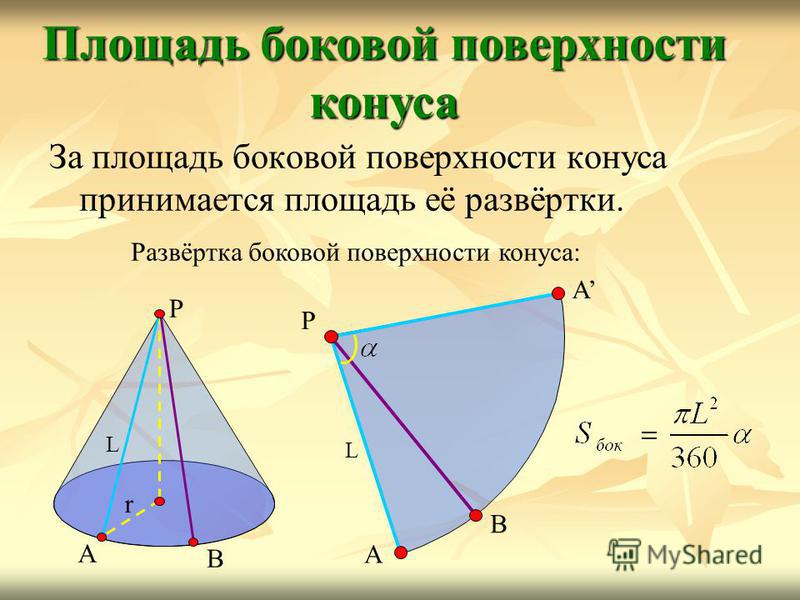
За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r
13
Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15
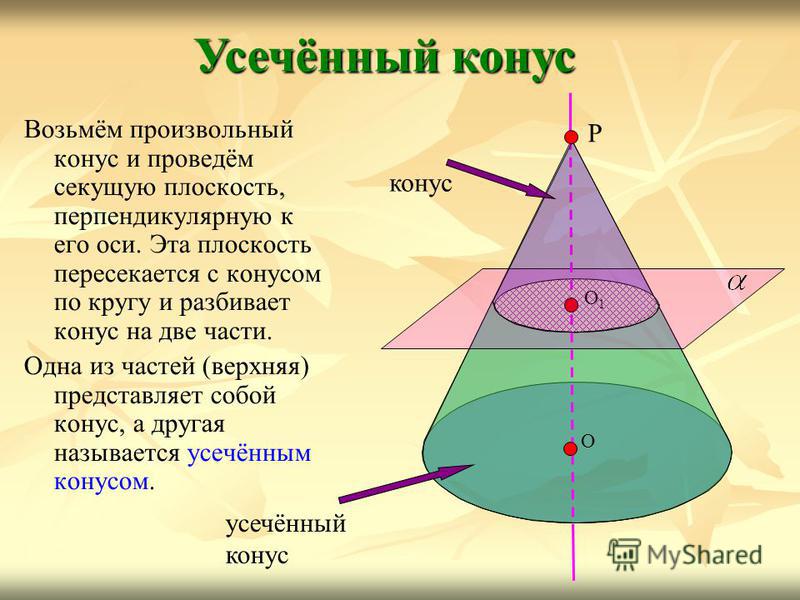
Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус
16
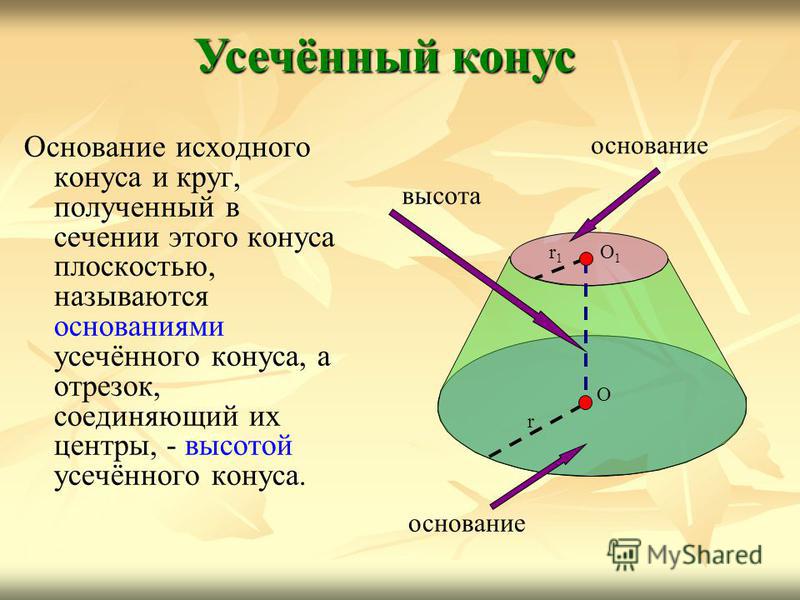
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота
17
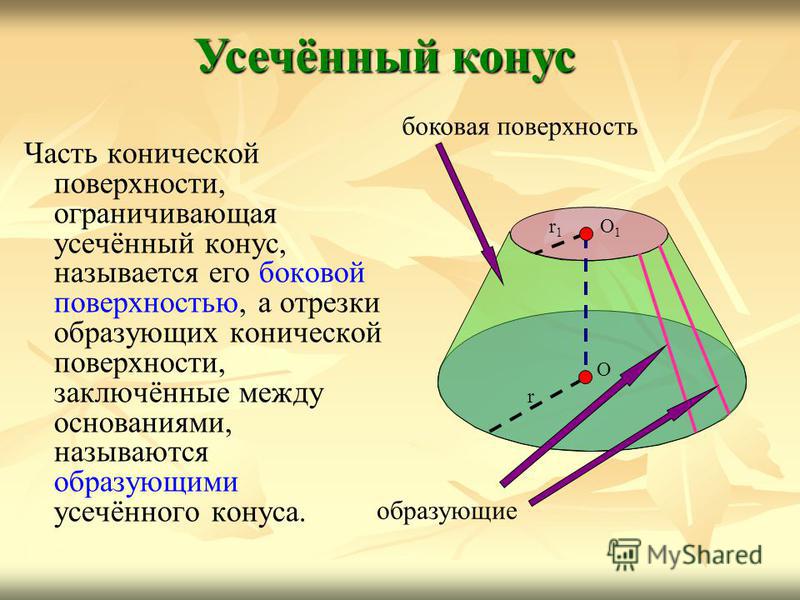
Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие
18
Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.
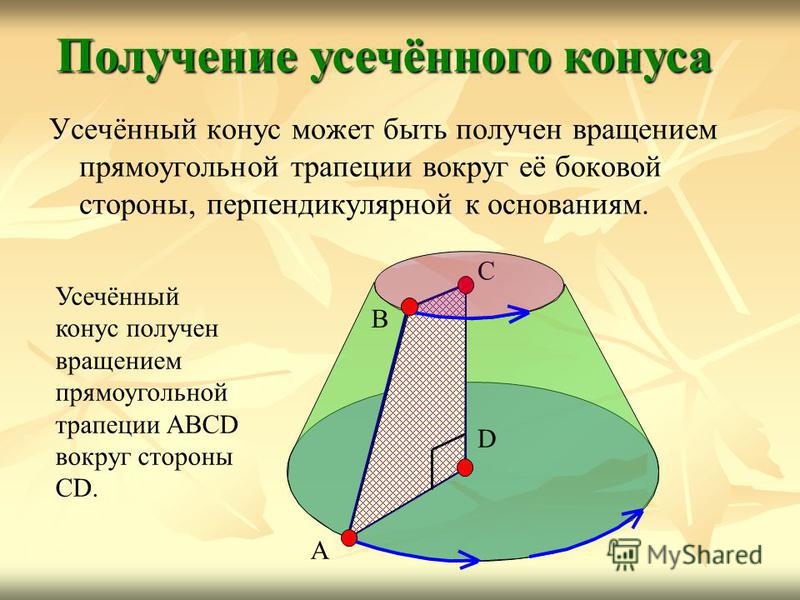
19
Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L
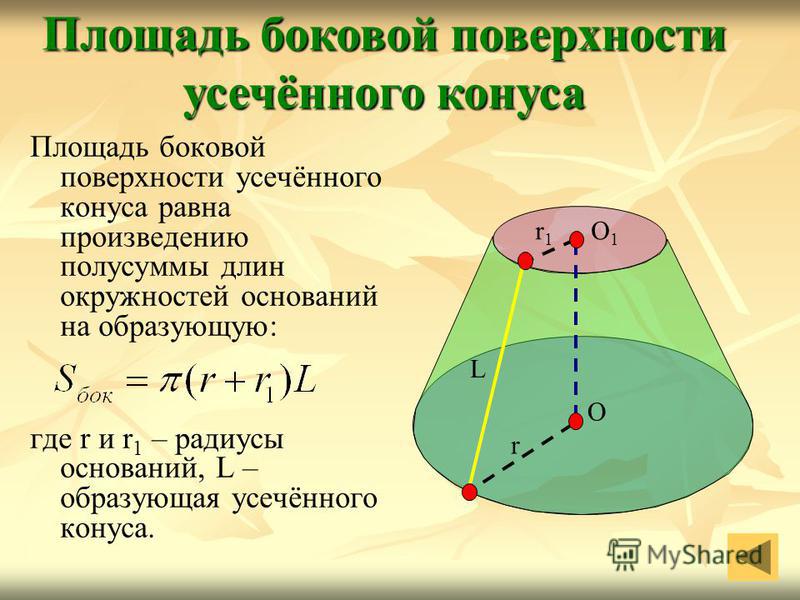
Генератриса усеченной фигуры
Итак, мы познакомились с усеченным конусом, а также с понятием о его образующей. Как находить образующую конуса усеченного? Для того чтобы получить нужную формулу, заметим, если высоту h перенести параллельно самой себе к боковой поверхности конуса так, чтобы она касалась одним концом образующей фигуры, то получится прямоугольный треугольник. Его сторонами будут высота h (катет), генератриса g (гипотенуза) и r1-r2 (катет). Тогда можно записать формулу для определения g:
g = √((r1 – r2)2 + h2)
Соответственно, если дан острый угол φ1 между большим основанием и генератрисой, тогда последнюю можно определить так:
g = h/sin(φ1);
g = (r1 – r2)/cos(φ1)
Если же известен тупой угол φ2 между малым основанием и генератрисой, тогда для ее вычисления необходимо применять такие выражения:
g = h/sin(φ2);
g = (r2 – r1)/cos(φ2)
Здесь первая формула является точно такой же, как для угла φ1, а во второй формуле радиусы в числителе поменялись местами.
Таким образом, найти образующую конуса усеченного можно, если знать любые три его параметра.
Определение диаметра через объем и высоту
Теперь покажем, как найти диаметр конуса, зная его объем V и высоту h. Для этого необходимо вспомнить, что объем конуса, как и объем любой пирамиды, можно определить, пользуясь следующим равенством:
Здесь S — площадь основания. Поскольку площадь основания в рассматриваемом случае является площадью круга, то это выражение можно переписать в таком виде:
Остается выразить отсюда радиус и умножить его в два раза, и мы получим ответ на вопрос о том, как найти диаметр конуса через величины V и h. Имеем:
Заметим, что в правой части получается размерность длины. Это доказывает правильность полученной формулы.
Все записанные в статье формулы для диаметра d фигуры также являются справедливыми для радиуса, который будет в два раза меньше диаметра.